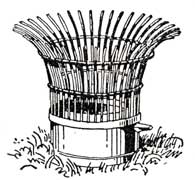
図5.2 小型蒸発計。口径20cm、高さ10cm の円筒形で真ちゅうまたは 黄銅製。小鳥が中の水を飲まないように針金で囲んである。
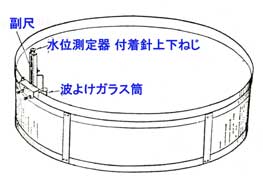
図5.3 大型蒸発計。口径120cm、高さ25cm の亜鉛鉄板製の円筒容器で、 白色塗装してある。約20cmの深さに水を入れる。水深測定用の ゲージ(水位測定器)とガラス円筒を取り付けてある。
著者:近藤純正 5.1 戦後の1950年前後の社会的状況 5.2 十和田湖の蒸発の研究 5.3 大気安定度の効果 5.4 実用化(バルク式の開発) 5.5 野尻湖の研究 5.6 熱収支的な考え方(ボーエン比の関係) 5.7 1960年代の社会的背景 5.8 高精度のための基礎研究 5.9 国際協力の気団変質観測研究
| トップページへ | 身近な気象の目次 | 次へ |
 図5.2 小型蒸発計。口径20cm、高さ10cm の円筒形で真ちゅうまたは 黄銅製。小鳥が中の水を飲まないように針金で囲んである。 |
 図5.3 大型蒸発計。口径120cm、高さ25cm の亜鉛鉄板製の円筒容器で、 白色塗装してある。約20cmの深さに水を入れる。水深測定用の ゲージ(水位測定器)とガラス円筒を取り付けてある。 |




 図5.10 野尻湖に建てた観測塔。 |
 図5.11 野尻湖での観測風景。 |


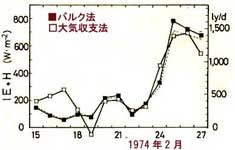 図5.19 海面熱収支量の比較1974年。縦軸は顕熱輸送量と潜熱輸送量の和、
横軸は2月の日付。
図5.19 海面熱収支量の比較1974年。縦軸は顕熱輸送量と潜熱輸送量の和、
横軸は2月の日付。
|
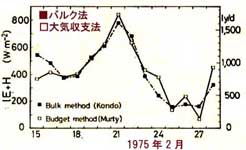 図5.20 海面熱収支量の比較1975年(Kondo, 1976,
J.Met.Soc.Japan.,382-398より引用)。
図5.20 海面熱収支量の比較1975年(Kondo, 1976,
J.Met.Soc.Japan.,382-398より引用)。
|
| トップページへ | 身近な気象の目次 | 次へ |