- オイラーの3体問題とは?
地球は太陽の周りを1年で公転している。では突如として巨大な別の天体、例えばブラックホールが出現して引力を及ぼしたら、地球の公転軌道はどうなるのだろうか。この様な課題は「オイラーの3体問題」と呼ばれる。計算を簡単にするため、ブラックホールは太陽に対して固定されているとみなし(太陽とブラックホールがお互いの周囲を円運動していると考える)、太陽とブラックホールの引力に我々の地球が翻弄されるという訳だ。
  
- 「オイラーの3体問題」を解析的に解くのは非常に難しい(というより私にはやり方の見当も付かない)が、数値的には比較的簡単に解くことが出来る。万物の創造主になった気分で地球の運命をもてあそぶ。考えただけでもワクワクする話ではないか。(しませんか?)
- 高校の物理で万有引力の法則を習った。万有引力は2つの物体の質量の積に比例し、距離の2乗に反比例するという。この法則を使うと、太陽と地球の質量・距離により万有引力が計算でき、これを地球の質量で割れば地球が運動する際の加速度が求まる。そして初速度を与えれば微少時間後の速度と位置が決まる。その新しい位置を基にして同じ計算を繰り返す。これで地球はめでたく太陽の周りを回るはずだ。そしてブラックホールが出現した場合、太陽とブラックホールからの引力をそれぞれxy成分に分けて足すだけだから話は単純だ。
- 1982年に大学生だった私は、当時出回り始めた「パソコン」なるものを使えばこの計算が出来るはずだと考え、無性にこれをやりたくて仕方がなくなった。たまたま近くの電気屋に当時は珍しかったパソコンのデモ機が置いてあるのを見つけたが、聞けばタダで使わせてくれるというではないか(誰も使わずに埃をかぶっていたのだ)。そこで私はBASIC言語をにわか勉強して、地球の公転プログラムを作ったのだった。
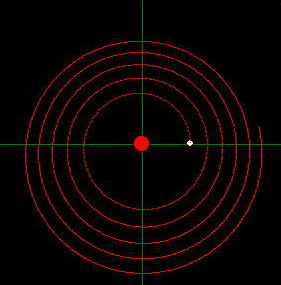
- ところがである。太陽と地球だけで計算しても地球の軌道が円にならない。蚊取り線香のように渦を巻いてしまうのだ。「微少時間」の設定が長すぎるのだろうと思い、これを短く設定しても全然駄目だった。原理的にはそれでうまく行くはずなのだが、この時に使ったBASIC言語は数字の精度が低く、却って誤差が増えてしまうためだった(NECのPC-6001に搭載されていたN60-BASIC)。
- 偉大なる「ルンゲ・クッタ法」
そんな時に見つけたのが、パソコンでの数値解析に適した「ルンゲ・クッタ法」なる近似法であった。このルンゲ・クッタ法の威力は絶大で、地球は見事に太陽をぐるりと一回りし、第2の天体を含めた計算も見事に成功した。ちなみに、Visual
Basicの様に精度の高い数字を使える処理系の場合は、微少時間を小さく設定すれば「ルンゲ・クッタ法」を使わなくてもうまく行く。
- ルンゲ・クッタ法を簡単に説明しておこう。
時刻 T での速度 = V(T)
時刻 T での位置 = P(T)
位置 P(T) での加速度 = A(P(T)) ← 万有引力の法則を用いる
として、
微少時間 dT 経過後の速度 V(T + dT)
微少時間 dT 経過後の位置 P(T + dT)
を求めればよいわけだ。
私が最初に試した単純な方法は「オイラー法」と呼ばれる。原理的には微少時間を小さく設定すればするほど正確に計算されるが、コンピューターで計算する際は有効数字の問題で誤差が生じたり、時間が長くかかるという欠点がある。
【オイラー法】
V(T + dT) = V(T) + A(P(T)) * dT
P(T + dT) = P(T) + V(T) * dT
これに対して、ルンゲ・クッタ法では以下で示すとおり4個の異なる点での加速度・速度を加重平均して計算するものだ。微少時間をそれ程小さくしなくとも高い精度で計算が出来る。
【ルンゲ・クッタ法】
V(T + dT) = V(T) + (V1 + 2 * V2 + 2 * V3 + V4) / 6
P(T + dT) = P(T) + (P1 + 2 * P2 + 2 * P3 + P4) / 6
V1 = A(P(T)) * dT
P1 = V(T) * dT
V2 = A(P(T) + P1 / 2) * dT
P2 = (V(T) + V1 / 2) * dT
V3 = A(P(T) + P2 / 2) * dT
P3 = (V(T) + V2 / 2) * dT
V4 = A(P(T) + P3) * dT
P4 = (V(T) + V3) * dT
この様な計算でどうして精度が高くなるのか、私にはとても証明できない。しかし万有引力の法則だって別に証明したわけでもないのだから、正しいと信じて使うことにする。
|

