- プログラムの検証
正三角形の3体問題
さて、この「N体問題プログラム」が正しく計算してくれるのかどうか検証してみよう。解析的に解を求められる単純な例を考えてみた。
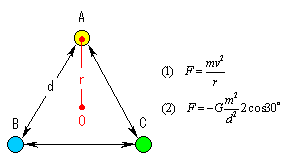
等しい質量(m)を持つ天体A、B、C、が正三角形の頂点に位置し、原点(O)を中心に半径(r)の回転運動をしている。この場合速度(v)で円運動を続けるための向心力(F)は(1)で求まる。また、他の2つの天体との間に働く万有引力(F)は(2)で求まる。そして両者が等しければA、B、Cは円運動を続けるはずだ。
これを天文単位(地球と太陽の距離を1、時間単位を1年にする)に置き換えて、r=1(太陽と地球の距離)、m=1(太陽の質量)であるとしてみよう。するとvが以下の通り求まる。
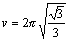 (単位は年) (単位は年)
- 計算通りに三つどもえ
そしてこれを使って試した結果が次の図である。
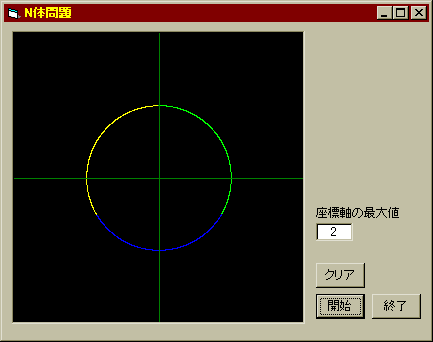
見事に3つの天体が文字通り三つどもえになって回転しており、この「N体問題プログラム」が正しく動いていることも証明されたわけだ。広い宇宙のどこかには、この様な「3つどもえ天体」も存在しているかもしれない。
- 遠方の巨大ブラックホール・・・
それでは太陽系を作って、はるか遠方の巨大ブラックホールの影響を見てみよう。「オイラーの3体問題」で試したものと同じ条件で、「地球の公転軌道半径の1000倍の距離(太陽から約1500億キロ、とは言ってもたかだか0.016光年)」に太陽の質量に比べて1000倍ものブラックホールが出現した場合をシミュレートしてみよう(ブラックホールの初速はゼロとした)。
- 影響が全くない?
ブラックホールが出現してから約20年経過した時点での様子が次の図である。中心に近い白い軌道(殆どつぶれており見えない)が水金地で、かろうじて赤く見えるのが火星の軌道。その周りでやっと分かれて見えるのが木星(ピンク色)、以下土星、天海冥と続く。
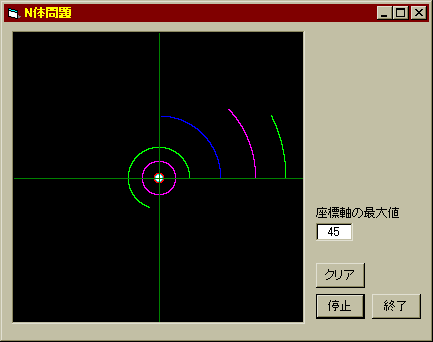
なんとブラックホールの影響は全く現れていないではないか!
- 重い天体も、軽い天体も、同じ速さで「落下」する
これらの軌道は常に太陽を原点に置いて描画している(ちなみに次の一行を追加するだけでよい)。
Set mobjSystem.DrawCenter = mobjSun
そして実はこの20年間に太陽系全体ではブラックホール方向に約13億キロも移動しているのだ(地球と太陽の距離の約8.5倍)。つまり太陽も他の9つの惑星と全く同様にブラックホールに引き寄せられており、太陽系全体では全く何事も起こっていないように見えるというからくりだ。その昔ガリレオが「重い物体も、軽い物体も、同じ速さで落下する」と言ったそうだが、これの宇宙版である。
ちなみに万有引力は距離の2乗に反比例するから「ブラックホールに近い物体は速く吸い込まれる」のだが、今回の例ではブラックホールが十分遠方にある為、太陽系全体にはほとんど同等に作用しているのだ。
何はともあれ巨大ブラックホールがはるか遠方に出現しても、我々の太陽系がすぐに壊滅する心配はしなくても良いのだ。これで杞憂が一つ減った。
- 小型ブラックホールが接近・・・
次はもっと深刻そうな例。太陽の2倍の質量のブラックホールが太陽系の外から近づいてきた場合をシミュレートしてみよう。
惑星の初期位置:X軸上の正方向に直列
ブラックホールの初期位置:(-40, 5) 太陽と地球の距離を1とする
40は冥王星、5は土星の公転半径に相当
ブラックホールの初速:(4, 0) 地球の公転速度の4倍
-
木星、土星よさらば・・・
まずは太陽を固定せず描画してみよう。左方向から右方向に向かって横に伸びている青い線がブラックホールの軌跡だ。太陽はこれに引かれて移動し、それにつられて地球(水色)や火星(赤色)も移動していることが分かる。木星と土星はどうやらはじき飛ばされてしまったようだ。
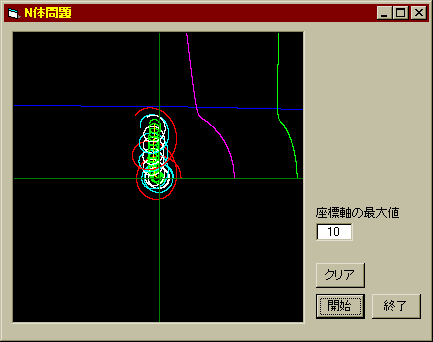
-
地球は無事だった
やはり地球人としては太陽との相対位置が気になるので、同じ条件で太陽を原点に置いて火星までを拡大して描画してみよう。
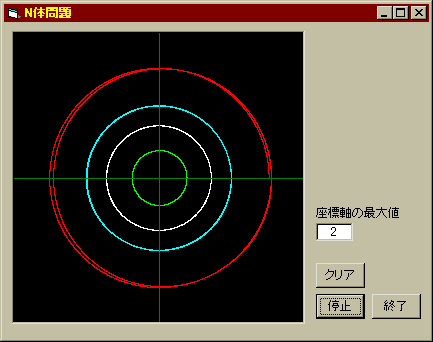
すると意外や意外、火星の軌道こそ僅かにずれているが、地球以下の軌道はほとんど影響を受けていないことが分かる。太陽の2倍くらいの質量のブラックホールがかなりニアミスを起こしたとしても、あまり心配しなくとも良さそうだ。ただしニアミスの相手が恒星だった場合は多少暖かくなるかもしれないが・・・・・
- 更に大型のブラックホールが接近
それでは一気に太陽の100倍の質量を持つブラックホールに登場願おう。位置などの初期条件は前回と同じだが、さすがに今回の影響は甚大で、惑星の動きたるや複雑怪奇だ。
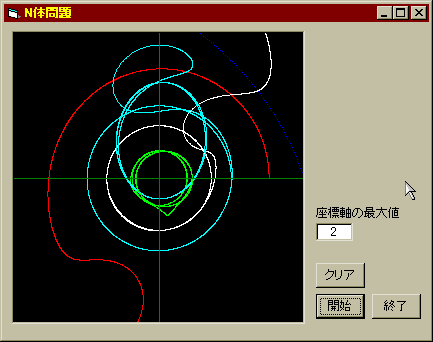
- 人類最後の日
まずブラックホールの軌跡が右上に見える。これは太陽を初めとする諸惑星が巨大質量のブラックホールに引き寄せられたことに他ならない。そして金星(白線)と火星(赤線)はどこぞへはじき飛ばされ、地球はいったん火星の軌道の外まで飛ばされた後で最終的には水星軌道と火星軌道までの距離を行き来する楕円軌道に落ち着いた。これでは灼熱地獄と寒冷地獄の行ったり来たりで、人類の滅亡は必至である。
広い宇宙にはブラックホールがうようよしているらしいから、これらが太陽系に近づかないことを祈るばかりだ。地球に巨大隕石が落ちれば人類は滅ぶし、ブラックホールが来れば太陽系は壊滅し、超新星の爆発が数百光年以内で起これば地球上は沸騰するそうだ。これらは杞憂よりは確率が高い。
- 2連星の太陽系
真円で回転する条件は?
今度は太陽とペアになって真円でお互いの周囲を回る2連星を考えてみよう。

上記の図にある2つの天体が等しい距離を保って回転する条件は以下の通りである。
(1)それぞれの天体の角速度が等しい
(2)それぞれの天体の向心力が等しい
(3)2つの天体の間に働く万有引力と向心力が等しい
この条件から立てた方程式を解くと太陽と相手の星(ペア星)の速度がそれぞれ次のように求まる。
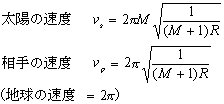
ちなみにMを太陽に比べて十分小さな値にとり、R=1とすれば太陽と地球がお互いの周囲を回転する条件が求まる。すなわち太陽の速度はゼロ、地球の速度は2piである。
- 太陽と同じ質量のペア星
それではまず太陽と全く同じ質量のペア星に登場願い、お互いの距離 R = 2 (太陽と地球の距離の2倍)を保って回転してもらおう。この様な連星系の惑星はどの様な軌道を描くのだろうか。
惑星に適当な初期位置と初速を与えた結果が以下の図である(X=0、Y方向速度=3pi)。黄色の太陽と青色のペア星が半径=1の円を描いて回転しており、水色の惑星が複雑な軌道を描いている。ちなみにこの惑星は青色のペア星の周りだけを公転しているのだ。どうやらなにがしかの規則性があるように見えるので調べてみよう。
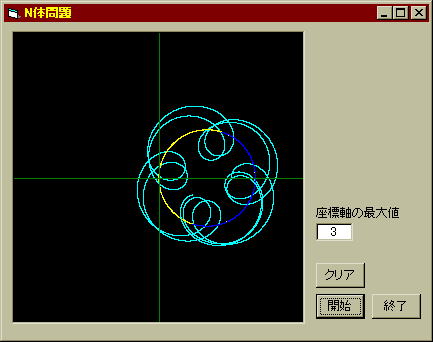
- ペア星を原点に固定して描画
では例によってペア星(青い軌道)を原点に固定して描画してみよう。太陽(黄色い軌道)が半径=2で周回しており、この惑星がペア星の周りだけを回っている事が分かる。惑星の軌道はペア星の周囲の大体同じ所に留まっていることが分かる。更に規則性を探し出してみよう。
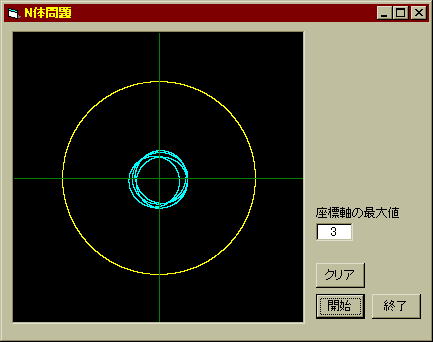
- 太陽もX軸上に固定して描画
今度は更に太陽もX軸上に固定して描画してみたのが下の図だ(これは前のページのプログラムには含まれていない機能だが)。つまり描画を原点を中心にして回転させ、太陽が常にX軸上に固定されるように補正するのだ。
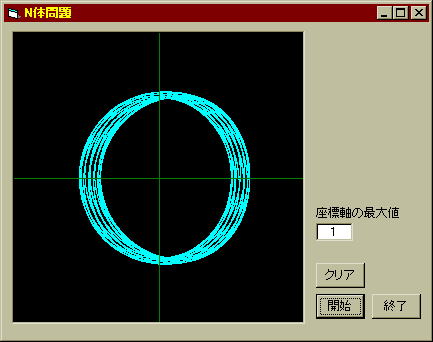
上の図ではペア星の周囲を回る惑星軌道を拡大しているが、太陽は右方向のX軸上に固定される様に補正されている。これから分かるとおり、ペア星の周りの公転軌道は太陽方向に近づいたり遠ざかったりを繰り返しているのだ。この様な惑星の住人には太陽の動きがとても複雑に見えることだろう。
- 惑星から見る2つの連星
惑星から見た連星の軌道を描いてみたのが次の図である。ペア星は少しずつずれる円を描くだけだが、他方の軌道はあたかも地球から見る惑星の軌道のようである。この様な連星系の惑星に住む天文学者は軌道計算に苦労することだろう。
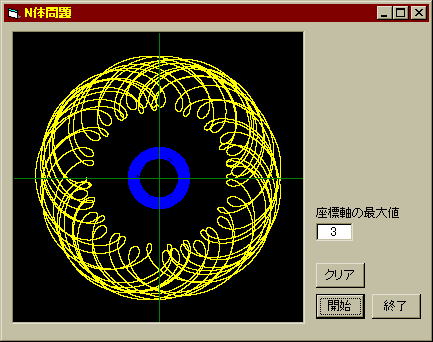
- 惑う星
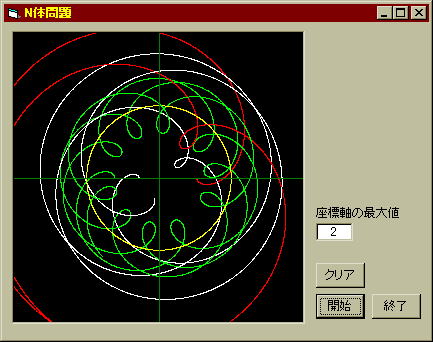
さて、次の図は一体どの様なブラックホールが来たのであろうか。答えは何でもない。普通の惑星の軌道を、地球を中心に描いてみたのだ。次の1行を追加するだけだ。
Set mobjSystem.DrawCenter = mobjEarth
赤が火星、白が金星、緑が水星だ。天動説ではこの軌道を体系的に説明しなければならないのだから大変だ。それにしても「惑星」とはよく言ったものである。ちなみに黄色い丸は言うまでもなく太陽である。
- まだまだ興味深い例はたくさんあるのだが、今回はこのくらいにしておこう。興味がある方は前のページのコーディングを基にしてご自分で試されることをお勧めする。
- 今後の改良点
この「N体問題プログラム」を改良するとしたら以下の様な点である。
- 3次元化
宇宙は(少なくとも)3次元だから、これを3次元に拡張したい。基本的には簡単な作業だが(x,
yにzを加えるだけの話)、同じ場所から眺めるだけではなくて色々と凝ってみたい。例えば地球を自転させてその視点から他の星を眺めるとか、太陽系に近づくブラックホールの位置から眺めるとか、考え出すとキリがない。
- 衝突時の処理
天体同士が衝突したときの処理をやりたい。とは言っても衝突時の複雑なシミュレーションなど出来ないから、Bodyオブジェクトに半径プロパティーを持たせ、それよりも近づいたら「軽い方のオブジェクトを削除」「重い方のオブジェクトに運動エネルギーを合体する」様な単純な処理を行わせるのだ。2つの太陽系を衝突させるシミュレーションなども面白いかもしれない(その手の本によれば、恒星同士がぶつかる確率は銀河系同士がぶつかる確率よりもずっと低いのだそうだが・・・)。
- 太陽系の惑星の位置を実物に合わせる
今回の例では9つの惑星の初期位置は「直列」状態である。つまり全てX軸の上からスタートするのだ。これを「200△年◎月□日の状態」で指定できるようにしたい。
3次元化の話とも共通するが、冥王星の軌道面は他の惑星の軌道面から大きくずれているのでこれもちゃんと処理したい。更に言えば惑星の軌道は楕円軌道なのでそれも正確に表現したい。特に冥王星はそれが著しい(海王星の内側に入ることすらある)。
・・・・でも「惑星の軌道要素」ってのはちらりと資料を見たが結構難しそうである。それに4次のルンゲクッタ法ってそこまで正確なのかという疑問は残る。
- 計算の間引きによる高速化 → 実施済
「N体問題」で万有引力の計算をする回数は「N x (N−1)」回だから、Nが増えるに従って指数関数的に増大する。これを解決する簡単な方法は、惑星のように太陽やブラックホールに比べて著しく質量が軽い天体は、相手の加速度に影響を及ぼさない事にするのだ。
これは思った以上に簡単な作業で、やってみたら僅か5分くらいで完成してしまった。Bodyクラスと全く同じ内容で「BodyLightクラス」を作り、軽い天体はこちらのクラスで実体を作るのだ。そしてSystemクラスでBodyLight用の機能をBodyオブジェクト用に倣って全く同じに作ればよい。こうすればBodyLightオブジェクトはBodyオブジェクトを対象に加速度を計算するが、BodyLightオブジェクトは自動的に計算の対象から外れるのだ。あっけない程の簡単さ・・・・
これを「オブジェクト指向」を使わずにやったら5分で済むだろうか?ここでも私は声を大にして言いたい。「オブジェクト指向プログラミング」の威力は絶大だ。
- 並列計算による高速化
Bodyオブジェクト1個分の計算は互いに独立して行い得るから、これらを並列的に計算させる事が出来れば高速化が可能だ。
マルチ・プロセッサーのPCは既にあるし、今後は1つのCPUにも複数の演算コアが含まれるようになるとも言われる。言語処理系(ないしOS)がこのマルチプロセッサーに対応してくれれば、劇的な高速演算が出来るようになるだろう。
- 私にとって「3体問題」や「N体問題」はプログラミングの原点であり、それだけに思い入れも深い。気が向いたときに取り組む日曜プログラマーの分際だが、これからも機会があれば改良を続けていきたいものだ。
|

