
17の原始根として 3 を選ぶ。
z17-1 = (z-1) (z16+ ... +z+1)
zk = exp (2πk/17) = cos(2πk/17) + sin(2πk/17).i (k=1, 2, ... , 16)
とする。
zk = z1k
となる。

17の原始根として 3 を選ぶ。
316 = 1 (mod 17)
原始根はどの値を選んでもよい(が、小さい値の方が計算が楽)。
17-1 = 2 * 2 * 2 * 2
(17-1)/2 = 8 ........... step 1
(17-1)/(2*2) = 4 ....... step 2
(17-1)/(2*2*2) = 2 ..... step 3
(17-1)/(2*2*2*2) = 1 ... step 4
より、長さ 8, 4, 2, 1 のガウス周期を順に作っていき、二次方程式を解いていく。
zk (k=1, 2, ... , 16) を2つの集合に分けて足す(長さ 8 のガウス周期を作る)。
p0 = z1 + z9 + z13 + z15 + z16 + z8 + z4 + z2
( = ∑ z32 i , i = 0 to 7 )
p1 = z3 + z10 + z5 + z11 + z14 + z7 + z12 + z6
( = ∑ z32 i + 1, i = 0 to 7 )
べきだけ書き下すと、
p0 : { 1, 9, 13, 15, 16, 8, 4, 2 } = { 30, 32, 34, 36, 38, 310, 312, 314 } (mod 17)
p1 : { 3, 10, 5, 11, 14, 7, 12, 6 } = { 31, 33, 35, 37, 39, 311, 313, 315 } (mod 17)
|
ガウス周期の作り方を、もう少し簡単に説明すると、 1, 3, 9, 27=10, 30=13, 39=5, 15, 45=11, 33=16, 48=14, 42=8, 24=7, 21=4, 12, 36=2, 6, 18=1 となり、 1, 3, 9, 10, 13, 5, 15, 11, 16, 14, 8, 7, 4, 12, 2, 6
という16個の数の列が得られる。
p0 : 1 から順に 1 つおきにとっていく とすると、上記のような、
p0 : { 1, 9, 13, 15, 16, 8, 4, 2 } = { 30, 32, 34, 36, 38, 310, 312, 314 } (mod 17) が得られる。 |
この p0, p1 について、
p0+p1 = -1 (1...16が全部出てくるので)
p0p1 = (計算すると) = -4
となるので、p0, p1 は、二次方程式、
p2+p-4 = 0
の解。
p0, p1 = (-1±sqrt(17))/2
図形的考察により(複素平面上の単位円上の p0, p1 の x 座標の比較により)、
p1 < p0
なので、
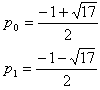
p0, p1 をさらに2つに分ける(長さ4のガウス周期を作る)。
q0 = z1 + z13 + z16 + z4
( = ∑ z34 i, i = 0 to 3 )
q1 = z3 + z5 + z14 + z12
( = ∑ z34 i + 1, i = 0 to 3 )
q2 = z9 + z15 + z8 + z2
( = ∑ z34 i + 2, i = 0 to 3 )
q3 = z10 + z11 + z7 + z6
( = ∑ z34 i + 3, i = 0 to 3 )
べきだけ書き下すと、
q0 : { 1, 13, 16, 4 } = { 30, 34, 38, 312 } (mod 17)
q1 : { 3, 5, 14, 12 } = { 31, 35, 39, 313 } (mod 17)
q2 : { 9, 15, 8, 2 } = { 32, 36, 310, 314 } (mod 17)
q3 : { 10, 11, 7, 6 } = { 33, 37, 311, 315 } (mod 17)
(注:それぞれ、足すと17になる組、2組から成っている)
ここで、
q0+q2=p0, q1+q3=p1
さらに、q0q2, q1q3は(計算すると)
q0q2= -1, q1q3= -1
となる。よって、q0 と q2, q1 と q3 はそれぞれ二次方程式、
q2-p0q-1 = 0 (q0, q2)
q2-p1q-1 = 0 (q1, q3)
の解。
q0, q2 = (p0±sqrt(p02+4))/2
q1, q1 = (p1±sqrt(p12+4))/2
ルートの中味を計算する。
![]()
とおくと、
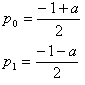
p0^2=(1+a^2-2a)/4=(1+17-2a)/4=(9-a)/2
p0^2+4=((9-a)+8)/2=(17-a)/2=(34-2a)/4
よって、
q0, q2={(-1+a)/2 +/- sqrt(34-2a)/2)}/2
={(-1+a) +/- sqrt(34-2a)}/4
図形的考察により、
q2<q0
∴
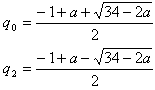
同様に、
p1^2=(1+a^2+2a)/4=(1+17+2a)/4=(9+a)/2
p1^2+4=((9+a)+8)/2=(17+a)/2=(34+2a)/4
よって、
q1, q3={(-1-a)/2 +/- sqrt(34+2a)/4}/2
={(-1-a) +/- sqrt(2(17+a))}/4
図形的考察により、
q3<q1
∴
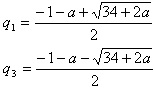
まとめると、
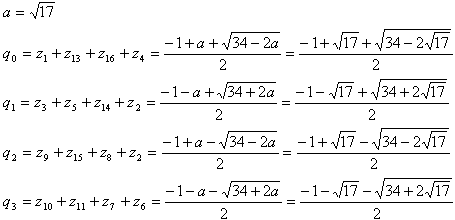
q0, q1, q2, q3 をさらに2つずつに分ける(長さ2のガウス周期を作る)。
r0 = z1 + z16
( = ∑ z38 i, i = 0 to 1 )
r1 = z3 + z14
( = ∑ z38 i + 1, i = 0 to 1 )
r2 = z9 + z8
( = ∑ z38 i + 2, i = 0 to 1 )
r3 = z10 + z7
( = ∑ z38 i + 3, i = 0 to 1 )
r4 = z13 + z4
( = ∑ z38 i + 4, i = 0 to 1 )
r5 = z5 + z12
( = ∑ z38 i + 5, i = 0 to 1 )
r6 = z15 + z2
( = ∑ z38 i + 6, i = 0 to 1 )
r7 = z11 + z6
( = ∑ z38 i + 7, i = 0 to 1 )
べきだけ書き下すと、
r0 : { 1, 16 } = { 30, 38 } (mod 17)
r1 : { 3, 14 } = { 31, 39 } (mod 17)
r2 : { 9, 8 } = { 32, 310 } (mod 17)
r3 : { 10, 7 } = { 33, 311 } (mod 17)
r4 : { 13, 4 } = { 34, 312 } (mod 17)
r5 : { 5, 12 } = { 35, 313 } (mod 17)
r6 : { 15, 2 } = { 36, 314 } (mod 17)
r7 : { 11, 6 } = { 37, 315 } (mod 17)
(注:それぞれ、足すと17になる組から成っている)
ここで、
r0+r4=q0, r1+r5=q1, r2+r6=q2, r3+r7=q3
さらに、r0r4, r1r5, r2r6, r3r7 は(計算すると)
r0r4=q1, r1r5=q2, r2r6=q3, r3r7=q0
となる。よって、r0 と r4, r1 と r5, r2 と r6, r3 と r7 はそれぞれ二次方程式、
r2-q0r+q1 = 0 (r0, r4)
r2-q1r+q2 = 0 (r1, r5)
r2-q2r+q3 = 0 (r2, r6)
r2-q3r+q0 = 0 (r3, r7)
の解。
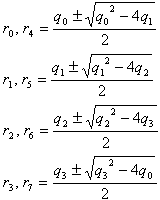
q02=(-1+a+sqrt(34-2a))2/16
=(1+a2+(34-2a)-2a+2a.sqrt(34-2a)-2sqrt(34-2a))/16
=(1+17 +34 -2a -2a+2a.sqrt(34-2a)-2sqrt(34-2a))/16
=(52-4a+2a.sqrt(34-2a)-2sqrt(34-2a))/16
![]()
q02-4q1={26-2a-sqrt(34-2a)+a.sqrt(34-2a)}/8 - (-1-a+sqrt(34+2a))
={26-2a-sqrt(34-2a)+a.sqrt(34-2a) +8(1+a-sqrt(34+2a))}/8
={26-2a-sqrt(34-2a)+a.sqrt(34-2a) +8+8a-8sqrt(34+2a)}/8
={34+6a-sqrt(34-2a)+a.sqrt(34-2a)-8sqrt(34+2a)}/8
![]()
∴
r0,r4=(q0+/-sqrt(q02-4q1))/2
={(-1+a+sqrt(34-2a))/4 +/- sqrt({68+12a-2sqrt(34-2a)+2a.sqrt(34-2a)-16sqrt(34+2a)}/16)}/2
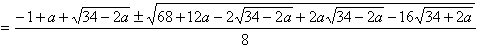
これで解が求められたが、いろいろな資料に出ている値、
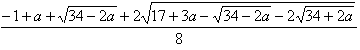
と見かけが異なる。計算してみると、値自体は正しい。
実は、a.sqrt(34-2a) を、sqrt(34-2a) と sqrt(34+2a) の一次結合で表すことができる。
a=sqrt(17)
a.sqrt(34-2a)=x.sqrt(34-2a)+y.sqrt(34+2a)
と置き、両辺をルート 2 で割ると、
a.sqrt(17-a)=x.sqrt(17-a)+y.sqrt(17+a)
両辺を2乗すると、
a2(17-a)= x2(17-a)+y2(17+a)+2xy.sqrt(172-a2)
= x2(17-a)+y2(17+a)+2xy.sqrt(172-17)
= x2(17-a)+y2(17+a)+2xy.sqrt(16.17)
= x2(17-a)+y2(17+a)+8xy.a
a と定数項の係数を比較すると、
x2+y2=17 ....... (1)
x2-8xy-y2=17 ... (2)
(1)から(2)を引く。
y(y+4x)=0
y=0 のとき、x2=17, x=sqrt(17)=a となり、自明な解となる。
y=-4x のとき、
x2+16x2=17
x=1, -1
x=1 のとき、y=-4 となるが、元の式に代入すると成り立たない。
x=-1 のとき、y=4 これは、成り立つ。
![]()
この値を代入する。最初に戻って、後ろのルートの中味
=68+12a-2sqrt(34-2a)-16sqrt(34+2a)-2sqrt(34-2a)+8sqrt(34+2a)
=68+12a-4sqrt(34-2a)-8sqrt(34+2a)
=4(17+3a-sqrt(34-2a)-2sqrt(34+2a))
よって、
r0,r4=(q0+/-sqrt(q02-4q1))/2
={(-1+a+sqrt(34-2a)) +/- sqrt(4(17+3a-sqrt(34-2a)-2sqrt(34+2a)))}/8
={(-1+a+sqrt(34-2a)) +/- 2sqrt(17+3a-sqrt(34-2a)-2sqrt(34+2a))}/8
となり、よく見かける式と同じ形になる。
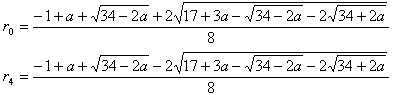
r0,r4=(q0+/-sqrt(q02-4q1))/2
r1,r5=(q1+/-sqrt(q12-4q2))/2
r2,r6=(q2+/-sqrt(q22-4q3))/2
r3,r7=(q3+/-sqrt(q32-4q0))/2
q02-4q1 と並行して、q12-4q2, q22-4q3, q32-4q0 の値を計算する。
a.sqrt(34+2a)=x.sqrt(34-2a)+y.sqrt(34+2a)
とおいて計算すると、
a.sqrt(34+2a)= 4sqrt(34-2a)+sqrt(34+2a)
となる。
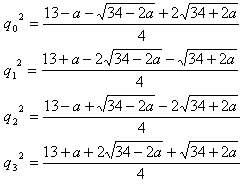
より、
q12-4q2=(13+a-2sqrt(34-2a)-sqrt(34+2a))/4 - 4(-1+a-sqrt(34-2a))/4
=(13+a-2sqrt(34-2a)-sqrt(34+2a)+4-4a+4sqrt(34-2a))/4
=(17-3a+2sqrt(34-2a)-sqrt(34+2a))/4
q22-4q3=(13-a+sqrt(34-2a)-2sqrt(34+2a))/4 - 4(-1-a-sqrt(34+2a))/4
=(13-a+sqrt(34-2a)-2sqrt(34+2a)+4+4a+4sqrt(34+2a))/4
=(17+3a+sqrt(34-2a)+2sqrt(34+2a))/4
q32-4q0=(13+a+2sqrt(34-2a)+sqrt(34+2a))/4 - 4(-1+a+sqrt(34-2a))/4
=(13+a+2sqrt(34-2a)+sqrt(34+2a))/4+4-4a-4sqrt(34-2a))/4
=(17-3a-2sqrt(34-2a)+sqrt(34+2a))/4
r0,r4=(q0+/-sqrt(q02-4q1))/2
={(-1+a+sqrt(34-2a)) +/- 2sqrt(17+3a-sqrt(34-2a)-2sqrt(34+2a))}/8
r1,r5=(q1+/-sqrt(q12-4q2))/2
={(-1-a+sqrt(34+2a)) +/- 2sqrt(17-3a+2sqrt(34-2a)-sqrt(34+2a))}/8
r2,r6=(q2+/-sqrt(q22-4q3))/2
={(-1+a+sqrt(34-2a)) +/- 2sqrt(17+3a+sqrt(34-2a)+2sqrt(34+2a))}/8
r3,r7=(q3+/-sqrt(q32-4q0))/2
={(-1-a-sqrt(34+2a)) +/- 2sqrt(17-3a-2sqrt(34-2a)+sqrt(34+2a))}/8
まとめると、

最後のステップ:z1, ... , z16 を求める。
r0=z1+z16, r4=z13+z4
r1=z3+z14, r5=z5+z12
r2=z9+z8, r6=z15+z2
r3=z10+z7, r7=z11+z6
z1+z16=2Re(z1) より、
Re(z1)=Re(z16)=r0/2
同様に、
Re(z3)=Re(z14)=r1/2, Im(z3, z14)= ±sqrt(1-(r1)2), Im(z3) がプラス
Re(z9)=Re(z8)=r2/2 , Im(z9, z8)= ±sqrt(1-(r2)2), Im(z8) がプラス
Re(z10)=Re(z7)=r3/2, Im(z10, z7)= ±sqrt(1-(r3)2), Im(z7) がプラス
Re(z13)=Re(z4)=r4/2, Im(z13, z4)= ±sqrt(1-(r4)2), Im(z4) がプラス
Re(z5)=Re(z12)=r5/2, Im(z5, z12)= ±sqrt(1-(r5)2), Im(z5) がプラス
Re(z15)=Re(z2)=r6/2, Im(z15, z2)= ±sqrt(1-(r6)2), Im(z2) がプラス
Re(z11)=Re(z6)=r7/2, Im(z11, z6)= ±sqrt(1-(r7)2), Im(z7) がプラス
虚部の符号は、上半平面にある z1, z2, z3, z4, z5, z6, z7, z8 がプラス、
下半平面にある z9, z10, z11, z12, z13, z14, z15, z16 がマイナスとなる。
r0=(-1+a+sqrt(34-2a))/8=s/8
とおくと、
Re(z)=r0/2=s/16
Im(z)=sqrt(1-s2/162)
=sqrt(162-s2)/16
となる。
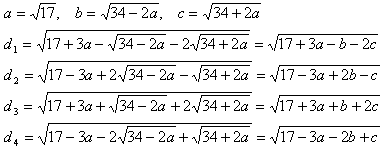
とおくと、r0, ... , r7 の分子は、
r0= -1+a+b+2d1, r02= 1+a2+b2+2ab-2a-2b+4d12-4d1+4ad1+4bd1
r4= -1+a+b-2d1, r42= 1+a2+b2+2ab-2a-2b+4d12+4d1-4ad1-4bd1
r1= -1-a+c+2d2, r12= 1+a2+c2-2ac+2a-2c+4d22-4d2-4ad2+4cd2
r5= -1-a+c-2d2, r52= 1+a2+c2-2ac+2a-2c+4d22+4d2+4ad2-4cd2
r2= -1+a-b-2d3, r22= 1+a2+b2-2ab-2a+2b+4d32+4d3-4ad3+4bd3
r6= -1+a-b+2d3, r62= 1+a2+b2-2ab-2a+2b+4d32-4d3+4ad3-4bd3
r3= -1-a-c-2d4, r32= 1+a2+c2+2ac+2a+2c+4d42+4d4+4ad4+4cd4
r7= -1-a-c+2d4, r72= 1+a2+c2+2ac+2a+2c+4d42-4d4-4ad4-4cd4
ab, ac は前の計算により、b と c の一次結合で表すことができる。
ab=a.sqrt(34-2a)= -sqrt(34-2a)+4sqrt(34+2a)=-b+4c
ac=a.sqrt(34+2a)= 4sqrt(34-2a)+sqrt(34+2a)=4b+c
dj2 (j=1,2,3,4) は、定数、a, b, c の一次結合
a2=17, b2=34-2a, c2=34+2a
a.dj, b.dj, c.dj (j=1,2,3,4) はこのまま
よって、ルート内は、
定数, a, b, c, dj, adj, bdj, cdj
の最大8つの項で構成されるはず。
r02= 1+a2+b2+2ab-2a-2b+4d12-4d1+4ad1+4bd1
= 1+17+34-2a+2(-b+4c)-2a-2b+4(17+3a-b-2c) -4d1+4ad1+4bd1
= 120+8a-8b -4d1+4ad1+4bd1
256-r02=256-(120+8a-8b -4d1+4ad1+4bd1)
= 136-8a+8b+4d1-4ad1-4bd1
= 4(34-2a+2b+d1-ad1-bd1)
ここで、d1-ad1-bd1 を簡略化することができる。
2乗すると、
(d1-ad1-bd1)2 = d12(1-a-b)2
= (17+3a-b-2c) (1+a2+b2-2a-2b+2ab)
= (17+3a-b-2c) (1+17+34-2a-2a-2b-2b+8c)
= (17+3a-b-2c) (52-4a-4b+8c)
= 272+48a+16b+32c
= 42(17+3a+b+2c)
ここで、d1-ad1-bd1 は負なので、
d1-ad1-bd1
= - sqrt((d1-ad1-bd1)2)
= - 4sqrt(17+3a+b+2c)
= - 4d3
実際に数値計算をやってみると、確かに、
d1-ad1-bd1 = - 4d3
であることがわかる。
以上より、
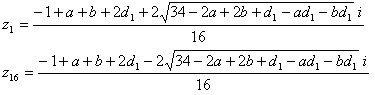
残りは、
r42= 1+a2+b2+2ab-2a-2b+4d12+4d1-4ad1-4bd1
= 1+17+(34-2a)+2(-b+4c)-2a-2b+4(17+3a-b-2c)+4d1-4ad1-4bd1
= 120+8a-8b+4d1-4ad1-4bd1
= 120+8a-8b-16d3
∴
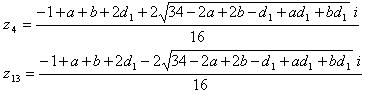
r12= 1+a2+c2-2ac+2a-2c+4d22-4d2-4ad2+4cd2
= 1+17+(34+2a)-2(4b+c)+2a-2c+4(17-3a+2b-c)-4d2-4ad2+4cd2
= 120-8a-8c-4d2-4ad2+4cd2
d2+ad2-cd2 も同じ要領で簡略化することができて、
d2+ad2-cd2 = -4d4
となる。よって、
120-8a-8c-4d2-4ad2+4cd2
= 120-8a-8c+16d4
∴
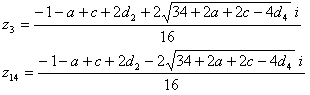
r52= 1+a2+c2-2ac+2a-2c+4d22+4d2+4ad2-4cd2
= 1+17+(34+2a)-2(4b+c)+2a-2c+4(17-3a+2b-c)+4d2+4ad2-4cd2
= 120-8a-8c+4d2+4ad2-4cd2
= 120-8a-8c-16d4
∴
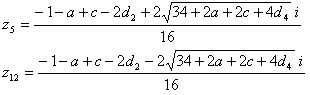
r22= 1+a2+b2-2ab-2a+2b+4d32+4d3-4ad3+4bd3
= 1+17+(34-2a)-2(-b+4c)-2a+2b+4(17+3a+b+2c)+4d3-4ad3+4bd3
= 120+8a+8b+4d3-4ad3+4bd3
= 120+8a+8b+16d1
∴
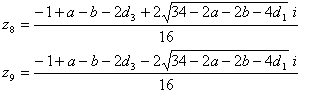
r62= 1+a2+b2-2ab-2a+2b+4d32-4d3+4ad3-4bd3
= 1+17+(34-2a)-2(-b+4c)-2a+2b+4(17+3a+b+2c)-4d3+4ad3-4bd3
= 120+8a+8b-4d3+4ad3-4bd3
= 120+8a+8b-16d1
∴
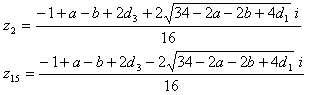
r32= 1+a2+c2+2ac+2a+2c+4d42+4d4+4ad4+4cd4
= 1+17+(34+2a)+2(4b+c)+2a+2c+4(17-3a-2b+c)+4d4+4ad4+4cd4
= 120-8a+8c+4d4+4ad4+4cd4
= 120-8a+8c+16d2
∴
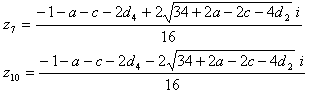
r72= 1+a2+c2+2ac+2a+2c+4d42-4d4-4ad4-4cd4
= 1+17+(34+2a)+2(4b+c)+2a+2c+4(17-3a-2b+c)-4d4-4ad4-4cd4
= 120-8a+8c-4d4-4ad4-4cd4
= 120-8a+8c-16d2
∴
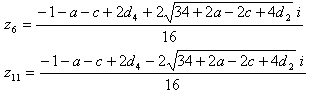
これで、16個全ての解を求めることができた。
16個の解を全部列挙すると、


z1だけ、a, b, c, d1, d2, d3, d4 を置き換えてみると、
(a=sqrt(17) だけは残しておく)
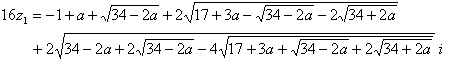
a=sqrt(17) も置き換えると、
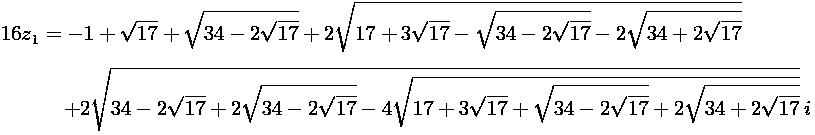
| back (Japanese) |
|---|