例題６

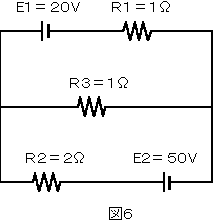
図６の回路において、抵抗Ｒ２を流れる電流を求めよ。ただし、電池の内部抵抗は
無視するものとする。

解説

まず最初に電流の方向を仮定します。
Ｉ１はＥ１のプラス側から流れるように、Ｉ２はＥ２のプラス側から流れるように、
またＩ１、Ｉ２がａ点に対して入ってきますからＩ３は、出て行く方向に仮定します。
電流を求める問題は、キルヒホッフの第一法則と第二法則の３つの閉回路のうち２つ
を用いて連立方程式で求めることができます。

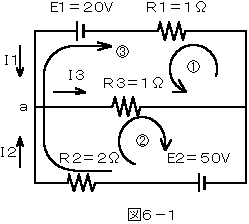
その１（図６−１）
キルヒホッフの第一法則と回路�@と回路�Aで解く方法

第１法則
　　　a点　Ｉ１＋Ｉ２＝Ｉ３ 　　　　　　　　・・・・・�@

第２法則
　　回路�@　Ｅ１＝Ｉ３・Ｒ３＋Ｉ１・Ｒ１　・・・・�A
　　回路�A　Ｅ２＝Ｉ２・Ｒ２＋Ｉ３・Ｒ３　・・・・�B

　　�A式及び�B式に�@式を代入すると、
　　　　　　　Ｅ１＝（Ｉ１＋Ｉ２）Ｒ３＋Ｉ１・Ｒ１　・・・・�C
　　　　　　　Ｅ２＝Ｉ２・Ｒ２＋（Ｉ１＋Ｉ２）Ｒ３　・・・・�D
　　�C式及び�D式に数値を代入して整理すると、
　　　　　　　２０＝２・Ｉ１＋Ｉ２　　　　　　　　　・・・・�E
　　　　　　　５０＝Ｉ１＋３・Ｉ２　　　　　　　　　・・・・�F
　　�F式をＩ１について整理すると、
　　　　　　　Ｉ１＝５０−３・Ｉ２　　　　　　　　　・・・・�G
　　�G式を６式に代入すると
　　　　　　　２０＝２（５０−３・Ｉ２）＋Ｉ２
　　　　　　　　　＝１００−６・Ｉ２＋Ｉ２
　　　　　　５・Ｉ２＝８０
　　　　　　∴　Ｉ２＝１６［Ａ］


その２（図６−１）
キルヒホッフの第一法則と回路�@と回路�Bで解く方法

第１法則
　　　a点　Ｉ１＋Ｉ２＝Ｉ３　　　　　　　　　　　　・・・・・�@

第２法則
　　回路�@　Ｅ１＝Ｉ３・Ｒ３＋Ｉ１・Ｒ１　　　　 ・・・・�A
　　回路�A　Ｅ２−Ｅ１＝Ｉ２・Ｒ２−Ｉ１・Ｒ１　・・・・�B

　　�A式に�@式を代入すると、
　　　　　　　Ｅ１＝（Ｉ１＋Ｉ２）Ｒ３＋Ｉ１・Ｒ１　・・・・�C
　　�C式及び�B式に数値を代入して整理すると、
　　　　　　　２０＝２・Ｉ１＋Ｉ２　　　　　　　　　・・・・�D
　　　　　　　３０＝２・Ｉ２−３０　　　　　　　 　・・・・�E
　　�E式をＩ１について整理すると、
　　　　　　　Ｉ１＝２・Ｉ２−３０　　　　　　　　　・・・・�G
　　�F式を�D式に代入すると
　　　　　　　２０＝２（２・Ｉ２−３０）＋Ｉ２
　　　　　　　　　＝４・Ｉ２−６０＋Ｉ２
　　　　　　５・Ｉ２＝８０
　　　　　　∴　Ｉ２＝１６［Ａ］

その３（図６−１）
キルヒホッフの第一法則と回路�Aと回路�Bで解く方法

第１法則
　　　a点　Ｉ１＋Ｉ２＝Ｉ３　　　　　　　　　　　　・・・・・�@

第２法則
　　回路�A　Ｅ２＝Ｉ２・Ｒ２＋Ｉ３・Ｒ３　　　　　・・・・�A
　　回路�A　Ｅ２−Ｅ１＝Ｉ２・Ｒ２−Ｉ１・Ｒ１　 ・・・・�B

　　�A式に�@式を代入すると、
　　　　　　　Ｅ２＝Ｉ２・Ｒ２＋（Ｉ１＋Ｉ２）Ｒ３　・・・・�C
　　�C式及び�B式に数値を代入して整理すると、
　　　　　　　５０＝Ｉ１＋３・Ｉ２　　　　　　　　　・・・・�D
　　　　　　　３０＝２・Ｉ２−Ｉ１　　　　　　　　　・・・・�E
　　�D式をＩ１について整理すると、
　　　　　　　Ｉ１＝５０−３・Ｉ２　　　　　　　　　・・・・�F
　　�F式を�E式に代入すると
　　　　　　　３０＝２・Ｉ２−（５０−３・Ｉ２）
　　　　　　　　　＝５・Ｉ２−５０
　　　　　　５・Ｉ２＝８０
　　　　　　∴　Ｉ２＝１６［Ａ］



その４（図６−２）
電流の方向をａ点から出て行く方向に仮定した場合

第１法則
　　　a点　Ｉ１＋Ｉ２＋Ｉ３＝０　　　・・・・・�@

第２法則
　　回路�@　Ｅ１＝Ｉ３・Ｒ３−Ｉ１・Ｒ１　　　　・・・・�A
　　回路�A　Ｅ２＝−Ｉ２・Ｒ２＋Ｉ３・Ｒ３　 　　　・・・・�B

　　�@式をＩ３について整理すると
　　　　　　　Ｉ３＝−（Ｉ１＋Ｉ２）　　　　　　　　　　・・・・�C
　　�A式及び�B式に�C式を代入すると、
　　　　　　　Ｅ１＝−（Ｉ１＋Ｉ２）Ｒ３＋Ｉ１・Ｒ１　 ・・・・�D
　　　　　　　Ｅ２＝Ｉ２・Ｒ２＋（Ｉ１＋Ｉ２）Ｒ３　　　・・・・�E
　　�D式及び�E式に数値を代入して整理すると、
　　　　　　　２０＝−２・Ｉ１−Ｉ２　　　　　　　　　・・・・�F
　　　　　　　５０＝−Ｉ１−３・Ｉ２　　　　　　　　　・・・・�G
　　�G式をＩ１について整理すると、
　　　　　　　Ｉ１＝−５０−３・Ｉ２　　　　　　　　　　 ・・・・�H
　　�H式を�F式に代入すると
　　　　　　　２０＝−２（５０−３・Ｉ２）−Ｉ２
　　　　　　　　　＝１００＋６・Ｉ２−Ｉ２
　　　　　　５・Ｉ２＝−８０
　　　　　　∴　Ｉ２＝−１６［Ａ］
　仮定した逆方向に１６［Ａ］流れます


どの方法でも求められますが、計算が簡単にできる方法を選ばれた方が良いでしょう。
この場合でしたらその１が良いと思います。

　例題７

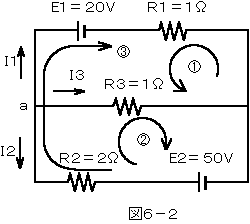
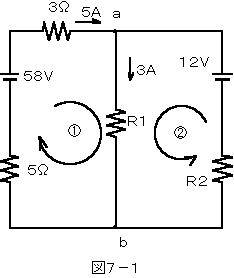
図７の回路において、矢印のような電流が流れているとき、抵抗Ｒ１で消費される電力を求めよ。ただし、電池の内部抵抗は無視するものとする。

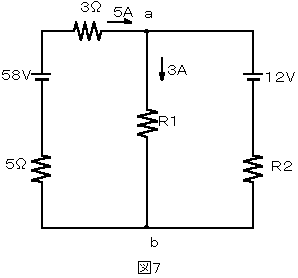
解説

図６−１のように、回路を流れる電流をＩ１、Ｉ２とすると、キルヒホッフの法則により次式が成り立つ。
　（３＋５）Ｉ２＋Ｒ１（Ｉ１＋Ｉ２）＝５８　　・・・・�@
　Ｒ２・Ｉ２＋Ｒ１（Ｉ１＋Ｉ２）＝１２　　　　・・・・�A
　Ｉ１＋Ｉ２＝３　　　　　　　　　　　　　　 ・・・・�B

 ここで、Ｉ１＝５［Ａ］及び�B式を�@式に代入すると、
　８・５＋３Ｒ１＝５８
　∴Ｒ１＝６［Ω］
従って、Ｒ１で消費される電力Ｐ１は、
   Ｐ１＝３×３×Ｒ１＝９×６＝５４［Ｗ］
以上は本に載っていた解説です。

このような問題はどこから解き始めたら良いのでしょうか。
まず最初にキルヒホッフの第二法則に従い、回路�@、回路�A、回路�B
をトレースして見ましょう。
回路�@はＲ１、回路�AはＲ１、Ｒ２とＩ、回路�BはＲ２とＩの値がわかりません。
また、電力はＶ、Ｉ、Ｒの３つのうち２つがわかれば求れこの問題の場合はＩがわ
かっているのでＶ１またはＲ１がわかれば求められます。
以上により回路�@から解き始めましょう。

�@式で３Ｒ１は電圧ですから、
　　　３Ｒ１＝１８［Ｖ］
Ｒ１で消費される電力Ｐ１は、
　　　　Ｐ１＝Ｖ・Ｉ＝１８・３＝５４［Ｗ］
でも良いと思います。

参考までに図６−２でキルヒホッフの法則を摘要すると次のようになります。

　　第一法則
　　５＝３＋Ｉ　　　　　　　　 　　　　　　・・・・ａ点
　　第二法則
　　５８＝（３＋５）・５＋Ｒ１・３　　　　・・・・１の回路
　　１２＝Ｒ１・３−Ｒ２・Ｉ　　　　　　 　・・・・２の回路
　　５８−１２＝（３＋５）・５＋Ｒ２・Ｉ　・・・・３の回路

　例題８

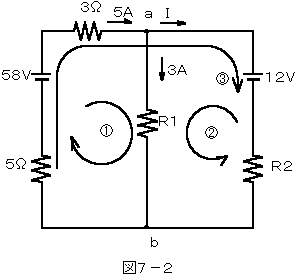
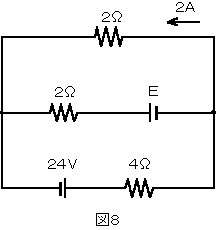
図８の回路において、起電力Ｅを求めよ。ただし、電池の内部抵抗は無視するものとする。

解説

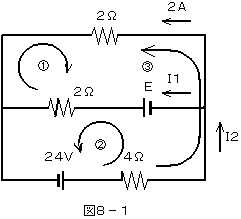
図８−１のように電流の方向を仮定します。
次にキルヒホッフの第二法則に従って回路�@、回路�A、回路�Bトレースして見ましょう。
回路�@はＥとＩ１、回路�AはＥとＩ１とＩ２、回路�BはＩ２の値がわかりません。
以上により回路�Bから始めましょう。

キルヒホッフの第二法則により回路�Bは
　　２４＝４・Ｉ２＋２×２　　　　　　　　　　　　・・・・�@
　　Ｉ２＝５［Ａ］

キルヒホッフの第一法則により電流は
　　２＋Ｉ１＝Ｉ２　　　　　　　　　　　　　　　　　・・・・�A

�A式にＩ２＝５［Ａ］を代入すると
　　Ｉ１＝３［Ａ］

キルヒホッフの第二法則により回路�@は
　　Ｅ＝２×Ｉ１−２×２
　　　＝２×３−２×２
　　　＝２［Ｖ］になります。

　例題９

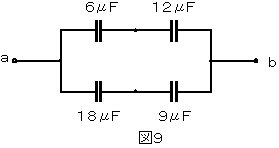
図９の回路において、端子ａ-ｂ間の合成静電容量を求めよ。

手順

（１）６μＦと１２μＦの合成静電容量求める。
（２）１８μＦと９μＦの合成静電容量求める。
（３）端子ａ-ｂ間の合成静電容量を求める。

解説

（１）直列の場合の合成静電容量は、各静電容量の和分の積で求められます。
　　６×１２／（６＋１２）＝４［μＦ］
（２）１８×９／（１８＋９）＝６［μＦ］
（３）並列の場合の合成静電容量は、各静電容量の和で求められます。
　　４＋６＝１０［μＦ］になります。

例題１０

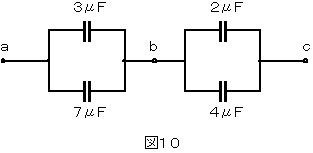
図１０の回路において、端子ａ-ｂ間に加わる電圧を求めよ。
ただし、端子ａ-ｃ間の電圧を１６０［Ｖ］とする。

手順

（１）端子ａ-ｂ間の合成静電容量を求める。
（２）端子ｂ-ｃ間の合成静電容量を求める。
（３）端子ａ-ｂ間に加わる電圧を求める。

解説

（１）並列の場合の合成静電容量は、各静電容量の和で求められます。
　　３＋７＝１０［μＦ］
（２）２＋４＝６［μＦ］
（３）直列回路の各コンデンサ端子電圧は、静電容量に反比例します。
　　　ａ-ｂ間に加わる電圧をＶ１、静電容量をＣ１
　　　ｂ-ｃ間に加わる電圧をＶ２、静電容量をＣ２、
　　　ａ-ｃ間に加わる電圧をＶとすると、
　　　Ｖ１：Ｖ２＝１／Ｃ１：１／Ｃ２
　　　Ｖ１：（Ｖ−Ｖ１）＝１／Ｃ１：１／Ｃ２
　　　Ｖ１／Ｃ１＝（Ｖ−Ｖ１）／Ｃ２
　　　両辺にＣ１・Ｃ２を掛けると
　　　Ｃ１・Ｖ１＝Ｃ２（Ｖ−Ｖ１）
　　　Ｃ１・Ｖ１＝Ｃ２・Ｖ−Ｃ２・Ｖ１
　　　（Ｃ１＋Ｃ２）Ｖ１＝Ｃ２・Ｖ
　　　Ｖ１＝Ｃ２・Ｖ／（Ｃ１＋Ｃ２）
　　　　　＝６×１６０／（６＋１０）
　　　　　＝６０［Ｖ］になります。
Ｖ１＝Ｃ２・Ｖ／（Ｃ１＋Ｃ２）は覚えておきましょう。
試験最中に計算したら効率が悪いです。

【ＴＯＰ】


copyright(C) 1998 mori! all rights reserved.