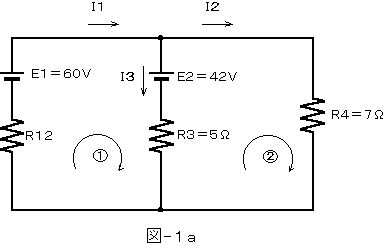
乮侾乯 愝栤偺夞楬偼恾亅侾倎偺夞楬偵抲偒姺偊傞偙偲偑偱偒傑偡丅
丂丂丂崌惉掞峈俼侾俀偼丄俼侾俀亖係亊侾俀乛乮係亄侾俀乯亖俁乵兌乶
丂丂丂恾亅侾倎偺夞楬偱僉儖僸儂僢僼偺戞侾朄懃傪揔梡偡傞偲丄
丂丂丂丂俬侾亖俬俀亄俬俁 丒 丒 丒 丒 丒 丒 丒 丒 嘆
丂丂丂嘆 偺夞楬媦傃嘇偺夞楬偱僉儖僸儂僢僼偺戞俀朄懃傪揔梡偡傞偲丄
丂丂丂丂俤侾亅俤俀亖俆俬俁亄俁俬侾
丂丂丂丂侾俉亖俆俬俁亄俁俬侾 丒 丒 丒 丒 丒 丒 丒 嘇
丂丂丂丂俤俀亖俈俬俀亅俆俬俁
丂丂丂丂係俀亖俈俬俀亅俆俬俁 丒 丒 丒 丒 丒 丒 丒 嘊
丂丂丂嘆 幃傪嘇幃偵戙擖偡傞偲
丂丂丂丂侾俉亖俆俬俁亄俁乮俬俀亄俬俁乯
丂丂丂丂侾俉亖俉俬俁亄俁俬俀
丂丂丂丂俬俁亖乮侾俉亅俁俬俀乯乛俉 丒 丒 丒 丒 丒 嘋
丂丂丂嘋幃傪嘊幃偵戙擖偟偰俬俀傪媮傔傞偲丄
丂丂丂丂係俀亖俈俬俀亅乷俆乮侾俉亅俁俬俀乯乛俉乸
丂丂丂丂俁俁俇亖俆俇俬俀亅俋侽亄侾俆俬俀
丂丂丂丂俈侾俬俀亖係俀俇
丂丂丂丂俬俀亖俇乵俙乶
乮俀乯
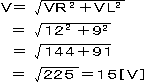
戞俀栤
乮俀乯揹埑憹暆搙偼丄擖椡怣崋揹埑傪倁倝丄弌椡怣崋揹埑傪倁倧丄揹埑憹暆搙傪俙倴偲偡傞偲偮偓偺傛偆偵側傝傑偡丅
丂丂丂丂俙倴亖倁倧乛倁倝
丂丂丂偙偺幃偵丄揹埑憹暆搙俆侽丄恾傛傝弌椡怣崋揹埑俀乵倁乶乮怳暆乯傪戙擖偟偰倁倝媮傔傞偲
丂丂丂丂俆侽亖俀乛倁倝
丂丂丂丂倁倝亖侽丏侽係乵倁乶亖係侽乵倣倁乶
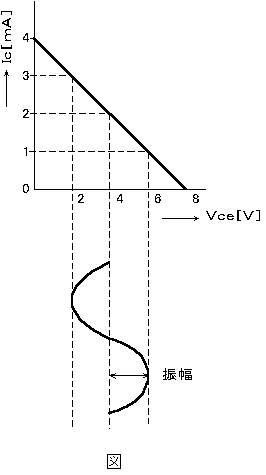
乮係乯俬倕亖俀乵倣俙乶丄俬們亖侾丏俋俇乵倣俙乶傛傝兛傪媮傔傞偲丄
丂丂丂兛亖俬們乛俬倕亖侾丏俋俇乛俀亖侽丏俋俉
丂丂師偵兝傪媮傔傞偲丄
丂丂丂兝亖兛乛乮侾亅兛乯亖侽丏俋俉乛乮侾亅侽丏俋俉乯亖係俋
戞俁栤
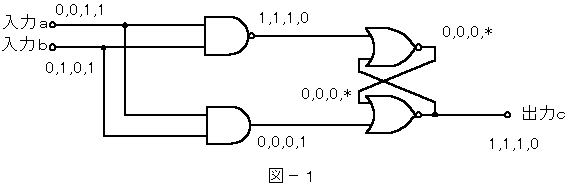
乮侾乯俶俙俶俢夞楬偺弌椡偼丄擖椡0,0,1,1,偲0,1,0,1傛傝1,1,1,0偵側傝傑偡丅
丂丂丂俙俶俢夞楬偺弌椡偼丄擖椡0,0,1,1,偲0,1,0,1傛傝0,0,0,1偵側傝傑偡丅
丂丂丂俶俷俼夞楬偼丄擖椡偺曅曽偵乽侾乿偑擖椡偝傟傞偲弌椡偼乽侽乿偵側傝傑偡丅偙傟傪忋偺俶俷俼夞楬偵揔梡偡傞偲丄擖椡1,1,1,0偐傜弌椡偼0,0,0,仏偵側傝傑偡丅
壓偺俶俷俼偺弌椡偼擖椡0,0,0,1偲0,0,0,仏傛傝1,1,1,0偵側傝傑偡丅
偟偨偑偭偰丄1,1,1,0傛傝斲掕榑棟愊偵側傝傑偡丅
乮俀乯 愝栤偺榑棟幃傪娙扨偵偡傞偲師偺傛偆偵側傝傑偡丅
丂丂丂丂
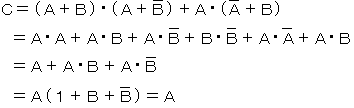
丂丂丂弌椡俠亖俙傛傝丄倂丄倃丄倄丄倅偼0,0,1,1偵側傝傑偡丅
乮俁乯榑棟夞楬偺擖椡倎偵0,0,1,1丄擖椡倐偵0,1,0,1傪擖椡偡傞偲弌椡們偼0,0,1,0偵側傝傑偡丅
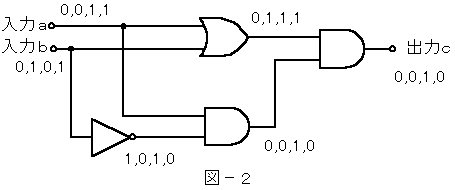
乮係乯愝栤偺恾偼丄壓恾偺傛偆偵暘夝偡傞偙偲偑偱偒傑偡丅
丂丂丂偙傟傪幃偱昞偡偲
丂丂丂丂俙丒俛亄俛丒俠亄俙丒俠偵側傝傑偡丅

戞係栤
乮侾乯 曄惉婍偺侾師懁偺揹埑傪倁侾丄俀師懁偺揹埑傪倁俀偲偡傞偲丄
丂丂丂丂倁侾丗倁俀亖俁丗係
丂丂丂丂係倁侾亖俁亊侾俇
丂丂丂丂倁侾亖侾俀乵倣倁乶
丂丂丂揹婥捠怣夞慄傊偺揹埑傪倁0丄曄惉婍偺侾師懁偺揹埑傪倁1丄揹婥捠怣夞慄偺懝幐傪俴偲偡傞偲丄
丂丂丂丂
丂丂丂偙偺幃偵奺抣傪戙擖偟偰俴傪媮傔傞偲丄
丂丂丂丂
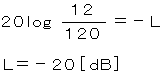
丂丂丂侾僉儘儊乕僩儖摉偨傝偺揱憲懝幐偼丄俀侽乛係侽亖侽丏俆乵倓俛乶