題意より端子a−b間の電圧がV、抵抗Rの両端の電圧がV/4
a−b間の合成抵抗がR、抵抗RとR2の合成抵抗が(R×R2)/(R+R2)
以上をまとめると
V:V/4=R:(R×R2)/(R+R2)
R=60を代入して解くと
V(60×R2)/(60+R2)=60V/4
(60×R2)/(60+R2)=15
60R2=15(60+R2)
60R2=900+15R2
45R2=900
R2=20[Ω]
◆◆ 問1(2) ◆◆
コンデンサの並列回路の合成リアクタンスをXcとすると、
Xc=(Xc1・Xc2)/(Xc1+Xc2)
=(120×120)/(120+120)
=60[Ω]
R−L−C回路の合成インピーダンスZは、
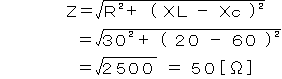
以上より、電流Iはオームの法則により、
I=V/Z=60/50=1.2[A]
抵抗Rにかかる電圧をVRとすると、オームの法則により
VR=I・R=1.2×30=36[V]
◆◆ 問2(3) ◆◆
コレクタ電流Icは、
Ic=α・Ie=0.98×1=0.98[mA]
電流増幅率βは、
β=α/(1−α)=0.98/(1−0.98)=49
ベース電流Ibは、
Ib=Ic/β=0.98/49=0.02[mA]=20[μA]
◆◆ 問3(2) ◆◆
論理式を論理代数の公式を用いて簡単にすると、下記のようになります。

◆◆ 問3(3) ◆◆
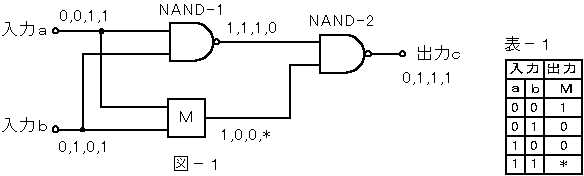
NAND−1の出力は、入力0,0,0,1と0,1,0,1により、出力cは1,1,1,0になります。
NAND回路は、両方の入力が1のとき出力が0に、片方でも0が入力されると出力は1になります。その性質を利用して、NAND−2に適用すると、入力1,1,1,0と出力0,1,1,1からもう一方の入力は1,0,0,*になります。(*は0か1)
この結果より論理素子Mに関して真理値表を作成すると表−1のようになり、これを満足させる論理素子はNORです。
◆◆ 問3(4) ◆◆
論理回路の入力aに0,0,1,1、入力bに0,1,0,1を入力すると出力cは次のようになります。
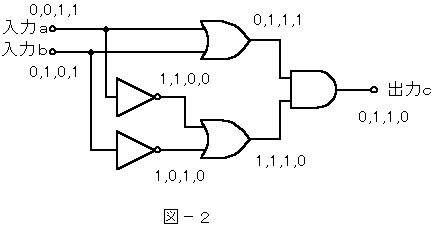
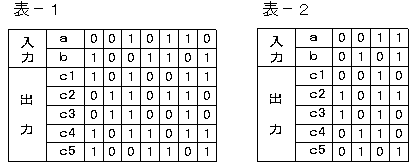
問題の図−3を置き換えると表−1のようになります。また、入力aが0,0,1,1、入力bが0,1,0,1を取り出すと表−2のようになり、 出力が0,1,1,0になるのは、c4になります。
◆◆ 問4(1) ◆◆
電気通信回線への入力電圧をV0、変成器の1次側にかかる電圧をV1、2次側にかかる電圧ををV2とし、電気通信回線の伝送損失をL、増幅器の利得Gとすると、発振器から1次側までの伝送量は、次のようになります。
また、伝送損失Lは、L=1.2×25=30[dB]、V0=240[mV]、G=10[dB]を上式に代入してV1を求めると、
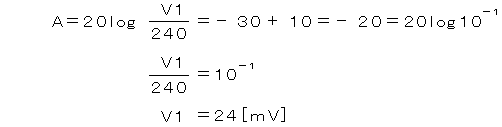
また、V1とV2の巻線比は4:3ですから次のような関係式が成り立ちなす。
V1:V2=4:3
上式よりV2を求めると、
4V2=24×3
V2=18[mV]
◆◆ 問4(2) ◆◆
A方向の漏話は近端漏話であり、この近端漏話減衰量をXは、送端電力をPs、近端漏話電力をPnとすると次のようになります。
X=10log(Ps/Pn)[dB]=10logPs−10logPn
この式にそれぞれ値を代入すると、
X=15−(−27)=42[dB]