|
金環食 赤経の合:1675年6月23日5時32分27秒(世界時)
|
| 35°N,135°E(≒京都) | 35°N,113°E(≒陽城) | 40°N,116°E(≒北京) | |
|---|---|---|---|
| 欠け始め | 6;34UT(15:34JST) | なし | 6:29UT |
| 食の最大 | 7:11UT(16:11JST) | なし | 6:40UT |
| 最大食分 | 0.126 | - | 0.009 |
| 欠け終り | 7:45UT(16:45JST) | なし | 6:50UT |
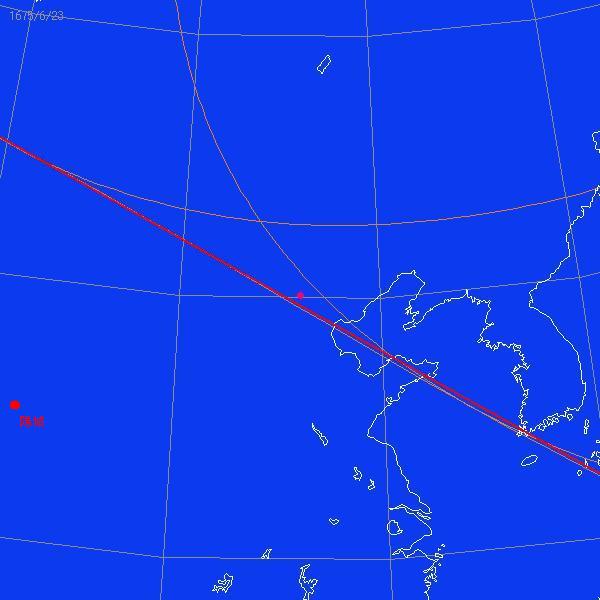
| 安井算哲(後の渋川春海)が授時暦を推挙していた延宝三年には五月一日に日食があったが、授時暦ではこれは予報されず、従来の宣明暦での予報が当たった。これを契機に算哲は授時暦に改良を加え、これが後の貞享暦となった。 しかし、この時の日食はどのようなものだったのか?はたして授時暦の予報は外れていたのか?以下ではこれについて検証してみる。 |
| グレゴリオ暦 | 宣明暦 | 授時暦 | 時憲暦 |
|---|---|---|---|
| 1675年6月21日 | 夏至? | ||
| 1675年6月22日 | 夏至? | ||
| 1675年6月23日(日食) | 五月一日 | 閏五月一日 | 閏五月一日 |
| 1675年6月24日 | 夏至 |
| ・ | 夏至は五月中気。宣明暦では五月二日が夏至。 |
| ・ | この時代、宣明暦の節気(平気法)は実際より2日ほど遅れていた。 授時暦の節気はかなり正しかったはず(ただし平気法としては)。 |
| ・ | (清朝)時憲暦(定気法)では夏至はさらに1日ほど早くなる(はず)。 |
|
金環食 赤経の合:1675年6月23日5時32分27秒(世界時)
|
| 35°N,135°E(≒京都) | 35°N,113°E(≒陽城) | 40°N,116°E(≒北京) | |
|---|---|---|---|
| 欠け始め | 6;34UT(15:34JST) | なし | 6:29UT |
| 食の最大 | 7:11UT(16:11JST) | なし | 6:40UT |
| 最大食分 | 0.126 | - | 0.009 |
| 欠け終り | 7:45UT(16:45JST) | なし | 6:50UT |

|
1.里差の導入 2.近日点の修正 |
| 里差 元 創為之○ 申時日食如三日月按宋史當紹聖元年是歳三月壬申朔食未六刻甚此 本朝與異方同日之食而加時差一辰此最為國差之證也○宋史曰 有食按此當 本朝寛元四年是時諸道勘申云申酉之間而蝕不正現獨算道主税頭雅衡云不可食果然乃賞之叙正四位下此則雅衡蓋知里差而言歟○武江與南部南北行程相距一百三十里北極出地差四度置相距里数以差度除之約三十許里而北極出地之差一度也○武江與津軽南北行程相距一百八十里北極出地差六度此亦約三十里為北極出地差度用乗三百六十五奇則知一周凡一萬一千里地厚凡三千五百里○用商尺六尺五寸為間六十間為町三十六町為里也 |
| 宣明暦、渤海より伝わる(862年行用)。 | |
| 耶律阿保機、契丹(後の遼)を建国(916)。 | |
| 契丹により渤海滅亡(926)。 | |
| 耶律楚材(阿保機の子孫)里差を提唱。 | |
| 渋川春海、貞享暦に里差を導入。宣明暦廃止(1685) |
| 時刻(UT) | 緯度 | 経度 | |
| 欠け始め | 3:40:29 | 26:9 S | 42:33 E |
| 皆既食の始め | 4:38:0 | 24:26 S | 28:7 E |
| 食の最大 | 6:23:37 | 6:3 N | 88:31 E |
| 皆既食の終り | 8:9:15 | 34:12 N | 155:43 E |
| 欠け終り | 9:6:51 | 32:29 N | 141:14 E |
| 日本(35°N,135°E) | 中国(35°N,120°E) | |
|---|---|---|
| 欠け始め | 6:35UT(15:35JST) | 6:19UT |
| 食の最大 | 7:43UT(16:43JST) | 7:32UT |
| 最大食分 | 0.952 | 0.849 |
| 欠け終り | 8:45UT(17:45JST) | 8:40UT |
| 国 | UT | 地方時 | 『貞享暦写本』 |
|---|---|---|---|
| 日本 | 7:43 | 16:43 | 申刻 |
| 宋 | 7:32 | 15:32 | 未六刻 |
| 時刻(UT) | 緯度 | 経度 | |
| 欠け始め | 4:32:33 | 19:48 S | 21:39 E |
| 皆既食の始め | 5:30:49 | 20:7 S | 6:58 E |
| 食の最大 | 7:17:22 | 19:39 S | 77:47 E |
| 皆既食の終り | 9:3:53 | 18:26 N | 134:21 E |
| 欠け終り | 10:2:4 | 18:45 N | 119:41 E |
| 日本(35°N,135°E) | 中国(35°N,120°E) | |
|---|---|---|
| 欠け始め | 7:59UT(16:59JST) | 8:1UT |
| 食の最大 | 8:51UT | |
| 最大食分 | 0.359 | |
| 食の終り | 8:20UT(17:20JST)(日没) | 9:20UT |
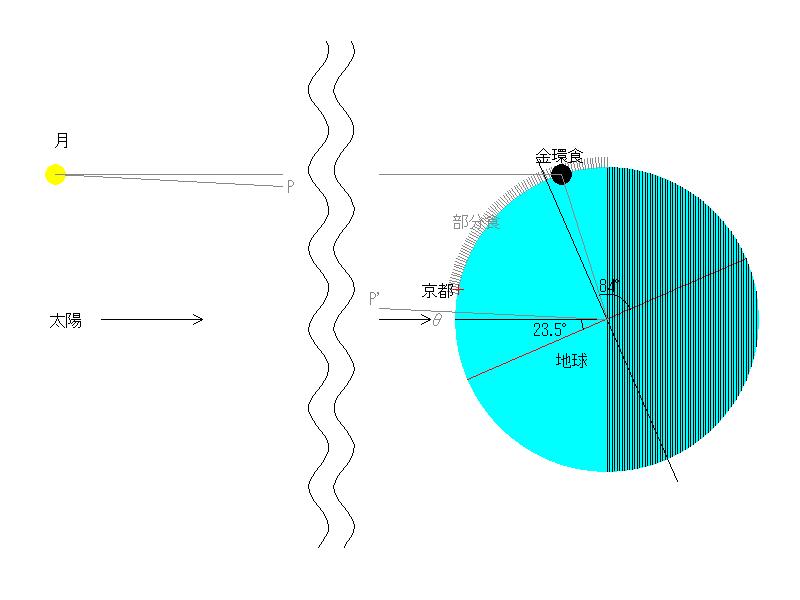
| さて近日点の平均黄経は,概略, 281°.22+6189″T+1″.63T2 で求めることができる。ただしTは1900.0年から計って100年を単位とする。授時暦採用の至元19年は1280年であるから,上式で計算すると,その頃の平均黄経は270.6度で,冬至点(270度)とほとんど一致している。そのため授時でも近日点と冬至点は一致しているとしている。・・貞享の頃は,近日点は277度にあり,そのために,延宝3年の授時による日食予報は失敗した。春海がこの近日点黄経の誤りに気付いたことは,里差(経度差)を考慮に入れたことと共に授時暦と貞享暦の大きな相違であろう。もちろん春海は授時暦の日食予報法に満足せず改良につとめたことは「授時暦固より古今に冠絶す。然し交食においては,少差無きこと能わざるなり」と言っていることで明らかである。 |
| その後春海は自ら観測を行い、宣明暦の誤りと授時暦・大統暦の正確さを立証した。しかし日月食の推算について、延宝三年(一六七五)五月朔日の日食については、授時暦では無食、宣明暦は二分半の食としたが、かえって宣明暦の方が蜜合した結果となった。この日食予報の失敗により、改暦のことは頓挫してしまった。 春海はこの度の失敗の原因は、授時暦が作られた一三世紀後半には冬至点と太陽の近地点がほとんど一致していたが、四〇〇年後の延宝三年には、近地点が冬至点から六度ほど前進していたことによる。春海はその事実を西洋天文学の成果を盛り込んだ「天経或問」(游子六著)によって知った。 |
|
内田正男編著『日本暦日原典』pp512 |
入気定日加減数は節気間の日数を示したものである。例えば1行目の「冬至・大雪」は、冬至〜小寒または大雪〜冬至の日数である。
この入気定日加減数はケプラーの法則とは一致しない。ケプラーより800年も前なので当然であろう。 これに「ケプラーのΔt式」を適用して最小二乗法によってeを求めると、 e≒0.021 これは実際の値(0.017)よりやや大きい。多少イビツな軌道である。 |
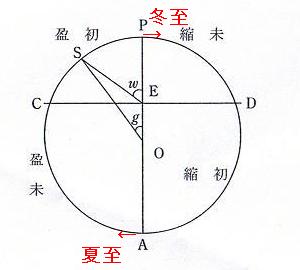 薮内清,中山茂『授時暦−訳注と研究』 アイ・ケイコーポレーション,2006年,pp10 | 授時暦の定朔は、「ギリシャ的な幾何学的モデルを使って」(中山)、図のように解釈できるという。 Oは太陽軌道P〜C〜A〜Dの中心、Eが地球である。OEは離心率であるが、ケプラーのそれと区別して、以下ではこれをe2とする。 gは平均黄経、wは実黄経に相当する。 であるから、 Δ=w−g とすると、 これとケプラーの黄経式を比べれば e2=2e である。 |
| 宣明暦(陽城時) | 授時暦 | 北大*(世界時) | 石原試算(中国時) |
|---|---|---|---|
| 13:12 | ? | 5:32:27 | 13:31 |
| 年/月/日 | 宣明暦 | 石原試算 |
|---|