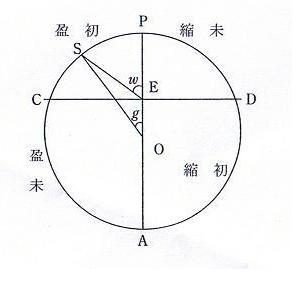
Oは太陽軌道P〜C〜A〜Dの中心、Eが地球である。OEは離心率であるが、ケプラーのそれと区別して、以下ではこれをe2とする。
gは平均黄経、wは実黄経に相当する。
であるから、
Δ=w−g
とすると、
これとケプラーの黄経式を比べれば
e2=2e
である。
| 允恭天皇三十四年乙酉 (445) |
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 同 三十五年丙戌 (446) |
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||
| 同 三十六年丁亥 (447) |
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||
| 同 三十七年戊子 (448) |
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||
| 同 三十八年己丑 (449) |
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||
| 同 三十九年庚寅 (450) |
|
|
|
|
|
|
|
|
|
|
|
|
|
| (1) | したがって、二九日の小の月と三〇日の大の月とを繰り返せば、ほぼ満足できるわけである。しかし、二朔望月の平均の長さは五九.〇六一一七八日だから、(略) したがって三三.三か月ごとに一日分となるから、大小大小大小・・・という組合せを三三カ月に一回大の月を重ねることでほぼ解消することになる | 岡田芳朗・伊東和彦・後藤晶男・松井吉昭 著『暦を知る事典』東京堂出版 2006年刊 |
| (2) | 「そこで昔の中国では、大小と規則的な組み合わせを十六回繰り返した後、連大といって、大の月を二回続けることによってこの端数を処理していた」 | 上田雄 著(石原幸男監修)『文科系のための暦読本』彩流社 2009年刊 |
| ・・・大小大・・・ |
| ↓ |
|---|
| ・・・大大大・・・ |
| ・・・小大小大小・・・小大小大小・・ |
| ↓ |
|---|
| ・・・小大大小大・・・大小大大小・・ |
| ・・・小大大小大・・・大小大大小・・ |
| 1<区> |
|---|
平朔
|
このシミュレーションでは初月初日を月齢0としたが、実際に月齢が0.0となることはきわめて珍しい。朔の日の月齢は0〜0.999のうちの<どこか>である。それが<どこ>なのかが決まらなければ以後の計算はできない。古い暦が上元を設けているのはこのためかと思われる。上元としては甲子夜半朔旦冬至という日が想定される。すなわち甲子の日の深夜(午前0時)に朔と冬至が重なるという非常に珍しい日で、たとえば宣明暦ではそれが700万年ほどの昔にあったとする。誰が見てきたんや、と思ってしまうが、ともかくそのような「暦の原点」を決めて、そこから平朔を求めたのであろう。なお、その日が甲子であるのは、かつて日は干支で数えたので、最初の干支である甲子から始めるのが計算上便利が良かったのだろう。 容易に想像できることだが、このように(平均)朔望月を積算していく方式なら、非常に長期についての1ヶ月の長さの平均はその暦法における朔望月に限りなく近付く。100ヶ月なら29.53日、1000ヶ月なら29.531日、10000ヶ月なら29.5306日・・・という具合である。 そして各暦法の平均朔望月は、日本で使われた最も古い元嘉暦でも現在の値と非常に近い。このため平朔に関しては長期の累積誤差もかなり小さい。元嘉暦と現在の差は0.000004日、したがって ヶ月(約20000年)で1日のずれである。これは節気(冬至)が宣明暦時代の800年ほどの間に2日近く遅れたのとは好対照である。
|
| 月の運動は不規則で、一般に秋から冬にかけては遅く、春から夏にかけては速い。 |
| λ= | 124°.8754+4812°.67881 T | (M-1) |
| +6°.2887 sin(338°.915 + 4772°.9886 T + A) | (M-2) | |
| +1°.2740 sin(107°.248 + 4133°.3536 T) | (M-3) | |
| +0°.6583 sin(51°.668 + 8905°.3422 T) | (M-4) | |
| +0°.2136 sin(317°.831 + 9543°.9773 T) | (M-5) | |
| +0°.1856 sin(176°.531 + 359°.9905 T) | (M-6) | |
| (以下略) |
| 項 | 微分項の振幅 |
|---|
|
|
入気定日加減数は節気間の日数を示したものである。例えば1行目の「冬至・大雪」は、冬至〜小寒または大雪〜冬至の日数である。
入気定日加減数は定気法による節気間隔のようなもの、と考えれば良い。ただし近日点は冬至に一致するとしている。実際の近日点は、古い時代には大雪付近にあったものが次第に動いて1300年頃に冬至点を通り、以後は小寒のほうへ動いている。なお、この節気間隔はケプラーの法則によるものと正確には一致しない。ケプラーより800年も昔の暦なのだから致し方なかろう。『ケプラーのΔt式』を用いて最小自乗法によって離心率eを求めると0.021ほどになる。実際のeは0.017ほどなので、これは2割ほど大きい。 |
| 宣明暦では、平気法の節気間隔(気策)は 一方、冬至〜小寒の日数は つまり、この間太陽は 速く動く。したがて14日目の太陽の位置は平気での である。したがって日数の差は このΔを角度に直せば これを 月の黄経速度−太陽の黄経速度 で割れば朔の時間補正値となる。ただし、月の黄経速度はおよそ13°/日なのに対し、太陽はおよそ1°/日であり、古来中国暦では後者を無視した。 月の黄経速度は であるが、宣明暦では恒星月は明らかにされていない。あえて求めるなら、 したがって補正値は 恒星月の代わりに近点月である暦周を用いると、 いずれも、入気定日加減数 434.6909分と正確には一致しない。しかし概ねこのような計算であろうと思われる。 入気定日加減数 434.6909分から恒星月を逆算すれば、 |

| 授時暦の定朔は、「ギリシャ的な幾何学的モデルを使って」(中山)、図のように解釈できるという。 Oは太陽軌道P〜C〜A〜Dの中心、Eが地球である。OEは離心率であるが、ケプラーのそれと区別して、以下ではこれをe2とする。 gは平均黄経、wは実黄経に相当する。 であるから、 Δ=w−g とすると、 これとケプラーの黄経式を比べれば e2=2e である。 |