ナンプレのルール

Number Place はルールにしたがって、９×９のマスに１〜９の数字をうめていくパズルです。そのルールは、

縦１列の中には重複した数はない。

横１行の中には重複した数はない。

太枠の中には重複した数はない。
の３つです。ルール自体は単純なので、パズル初心者でも気軽に取り組めると思います。

ナンプレの解法

私の知っているナンプレの解法を簡単に説明します。
カッコ内の呼び名は私が勝手に読んでいる呼び名です。 他でつかっても話は通じないので注意してください。(笑)

解法１（ここ）

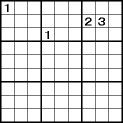最も基本の解法だと思います。
右上ブロックを見た時、「１」の入る場所は（２行、９列）しかありません。 第１行、第３行はそれぞれ左上ブロック、中上ブロックの「１」に邪魔されています。

「月刊ナンプレ」の初級問題のほとんどはこの手法のみで解くことが出来ます。 もちろん、別の手法を合わせて使ったほうが「速く」解けますが。

解法２（び〜）

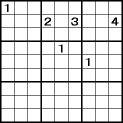解法１をちょっとひねった解法です。
まず中上ブロックに注目します。
左上ブロックの第１行、中中ブロックの第５列に「１」があるので、中上ブロックの「１」は（３行、４列）か（３行、６列）のどちらかになります。
ここで、視点を右上ブロックに変えます。
第１行は左上ブロックの「１」に邪魔され、中上ブロックの「１」は２点のどちらにしろ第３行になり、左上ブロック第３行を邪魔します。
そして、第７列は右中ブロックの「１」に邪魔されるので、結果的に残る場所は（２行、８列）しかなくなります。

解法２’（び〜・び〜）

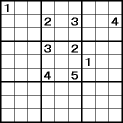解法２の応用篇です。
まず中中ブロックに注目します。
中中ブロックでは右中ブロックの「１」に邪魔されるため、「１」が入るのは（４行、５列）か（６行、５列）のどちらかになります。 そう、どちらにしろ「１」は第５列に入るのです。
次いで中上ブロックに注目します。
後は解法２で述べたとおりの手順で解くことが出来ます。

私が一番好きな解法です。 ３重ぐらいに重なった応用篇に気づいた時は思わずにんまりしてしまいます。

解法３（いちにっさん）

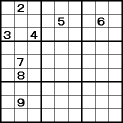「これ以外は入らない」数字を探す解法です。
（２行、２列）に注目します。
２、３、４は同じブロックにあるので×。 ５、６は同じ行にあるので×。 ７、８、９は同じ列にあるので×。
結局のところ（２行、２列）には「１」しか入る余地はありません。

「月刊ナンプレ」の中級問題の大半は以上の解法１、解法２、解法２’、解法３で解くことが出来ます。

解法４(L2,L3,L4)

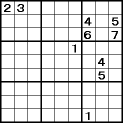「２つの数字が２マスのどちらかに入る場合、他の数字は入ることが出来ない」って云う、文章で書くと何云ってるんだか判らない解法です。
第８列に注目します。
右下ブロックにはすでに１があるので、（７行、８列）（８行、８列）（９行、８列）のいずれにも「１」は入りません。 また、中中ブロックの第４行に１があるので（４行、８列）にも「１」は入りません。 ここまでで、「１」の入る余地があるのは（１行、８列）（２行、８列）（３行、８列）のいずれかになります。
ここで、視点を変えて右上ブロックの２、３について調べてみます。
左上ブロックの第１行に２、３があるので２、３は第１行にはいることが出来ず、２つとも（２行、８列）か（３行、８列）に入ることになります。 ２が（２行、８列）なら３は（３行、８列）で、２が（３行、８列）なら３は（２行、８列）です。 （２行、８列）に２か３以外の数字が入ることはありません。 他の数字が入ってしまうと、右上ブロックで２もしくは３の入る余地がなくなってしまうからです。
ということで、（２行、８列）（３行、８列）には「１」が入ることができません。 従って、第８列で「１」が入るのは(入ることができるのは)（１行、８列）になります。
この辺になると、ちょっとこみいっていて、うまく説明することが出来ず判りにくいかもしれません。

解法５(Co2,Co3,Co4)

解法４の裏の考え方です。
２つの数字が２マスを独占するとき、その２つの数字は他のマスには入らない。
一般には解法４よりこの解法５の方が先に評価されると思います。 私はこの解法を理解するまでに十年以上かかりました。(苦笑)　 まだ理解したてなので、うまく説明できません。(^^;

解法番外編

背理法です。仮定法と呼ぶ人もいます。
パズルの問題は一意(Unique)に答えが決まります。 答えが一意でないものはパズルとして成立していないことになります。 ナンプレもパズルの一種ですから答えはひとつです。
適当に数字を当てはめてマスが全部埋まったら、それが答えです。
あるマスに入る可能性があるのが２と３だったとします。 まず２を入れて解いてみて矛盾がなく解ければそれが答えです。 途中で矛盾が出てくればそこは２ではなく３です。

背理法を使えばどんな問題も比較的簡単に解くことが出来ます。 でもそれは、私には「ナンプレの面白さを半減」させているように思えるので、私は一切背理法を使いません。 「月刊ナンプレ」の全問題も背理法を使わずに解けるようになっています。
ただ、ナンプレを解く楽しみは人それぞれなので、他の人が背理法を使うのは否定しません。 問題が解けないより、解けたほうが楽しいに決まってますから。

ここにあげた解法がナンプレの全解法ではありません。 他にもっと沢山の解法があります。
このページも、例題が見つからなかったり、うまく説明できない解法については載せていません。 自分の文才のなさを「自分で解法を見つけるのもナンプレの楽しさのひとつ」と云う言い訳に置き換えさせてもらいます。(笑)
うまい例題が見つかったら、また更新します。