対称群${S_n}$は、${n}$コの文字${\{1, \ 2, \ 3, \ \cdots, \ n \} }$の置換全体からなる群である。 群の要素（元）の数は、${\displaystyle n! }$である。これらは互換の積で表すことができる。 この中で偶数個の互換の積（偶置換）の集合の作る部分群が交代群${A_n}$で、その要素の数は ${\displaystyle \frac{n!}{2}}$である。
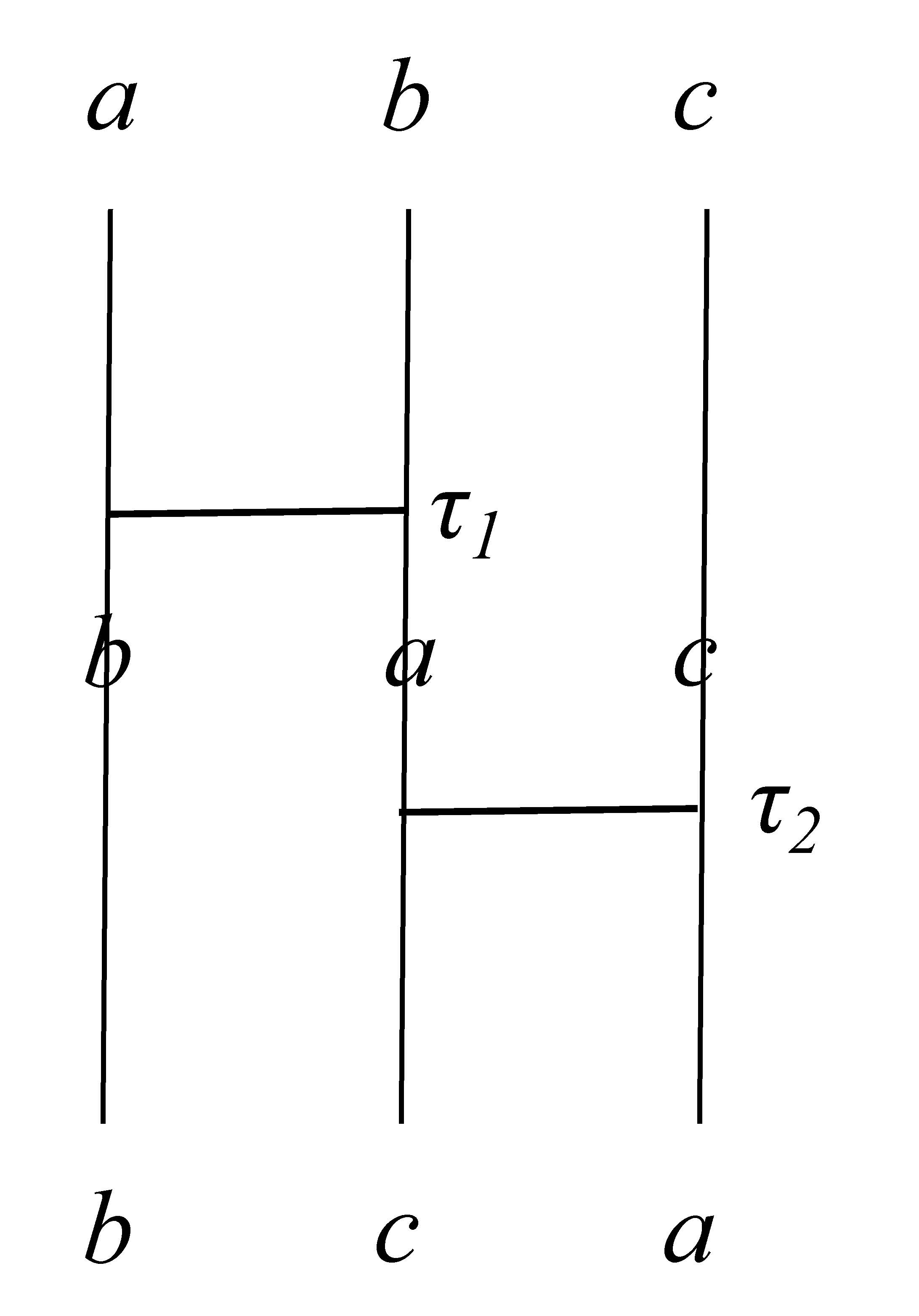
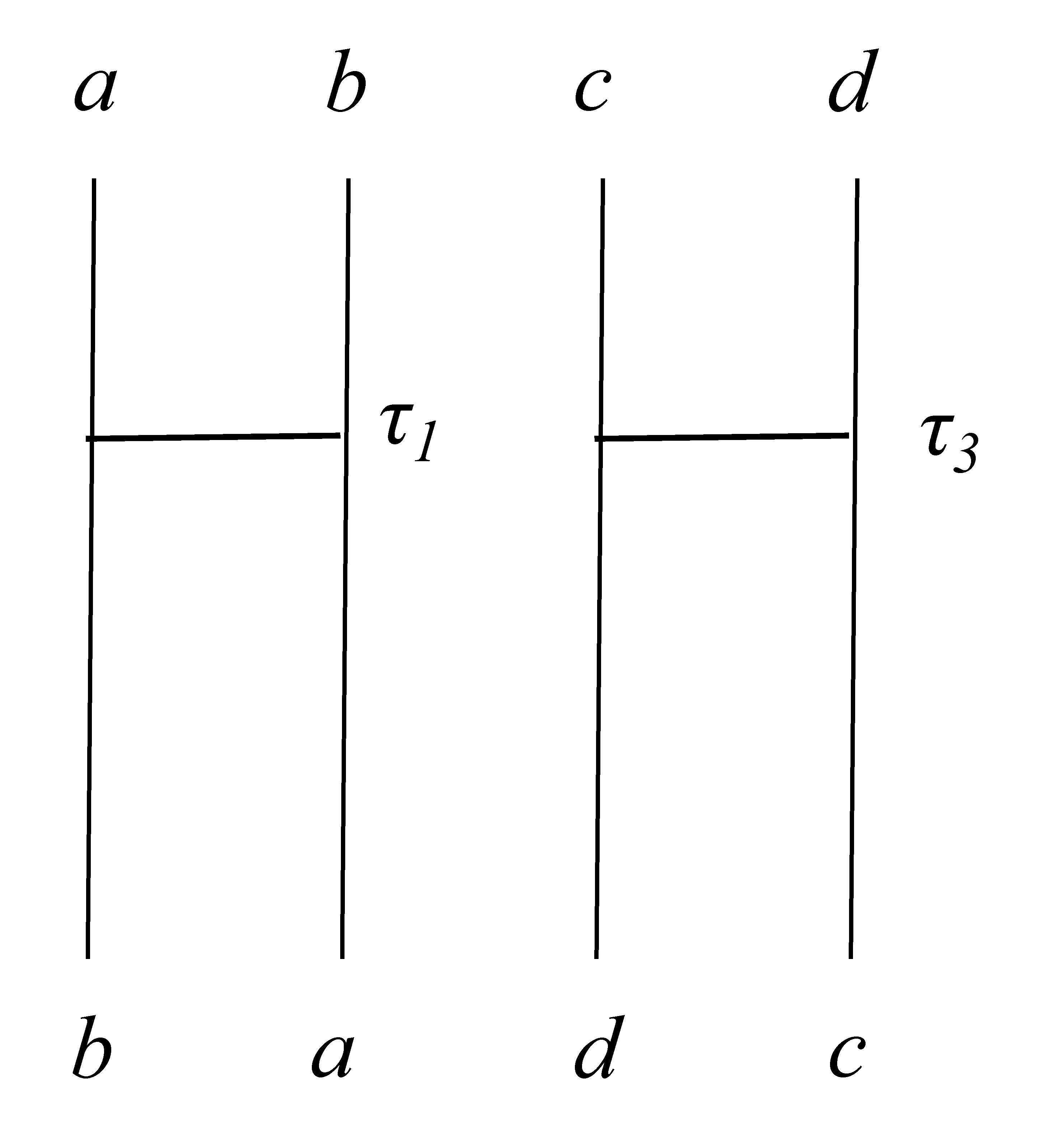
　全ての${A_n}$の要素を用いて互換のペアを作ることができる。2つのペアの積は、あみだくじを用いて図示すると、 同じ数を含む場合（図 1）と全ての数が異なる場合(図 2)の二通りがある。
　交代群${A_n}$は、${n \ge 3}$の場合、3サイクル（3次巡回置換）で生成されることを示す。そのためには、 互換の積は3サイクル（3次巡回置換）、またはそれらの積で表されることを示せば十分である。 置換の演算には、2通りの流儀があるが、ここでは、 置換${\pi_1}$を施してから置換${\pi_2}$を行う操作を ${ \pi_2 \pi_1 }$ と書くことにしよう。

• 2つの互換が同じ数${a}$を含む場合
　 2つの互換を \begin{equation} \tau_1 = (a \ b), \ \ \tau_2 = (a \ c) \end{equation} とおこう。 この時、 \begin{eqnarray*} \tau_2 \tau_1 &=& (a \ c)(a \ b) \\ &=&(a \ b \ c) \end{eqnarray*}
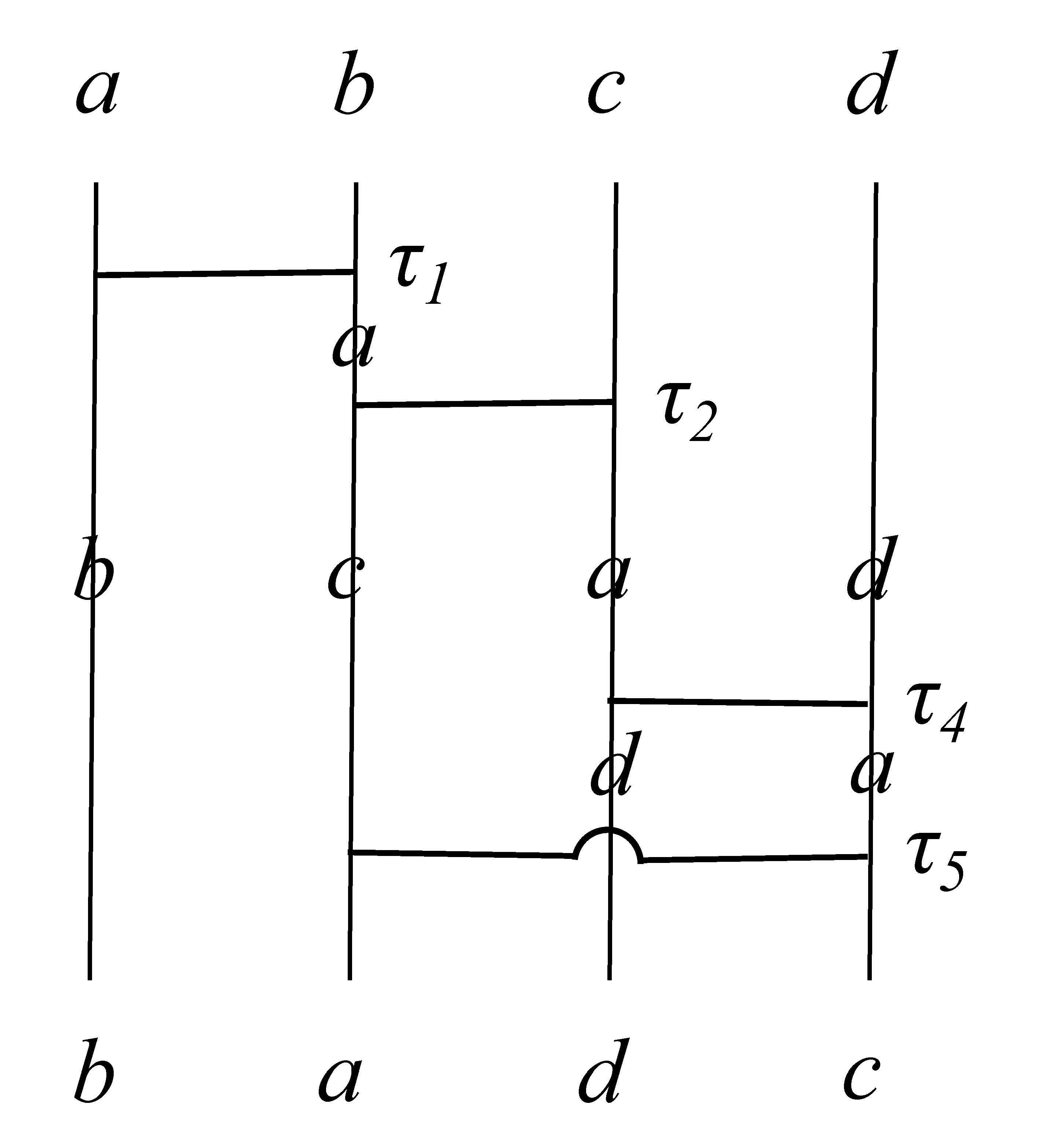
• 2つの互換が同じ数を含まない場合
　 この場合、 ${ \tau_3 = (c \ d) }$ とおいて${\tau_3\tau_1}$を調べよう。図 2 の結果は、図 3においても再現できるので、 \begin{eqnarray*} \tau_3\tau_1 &=& \tau_5\tau_4\tau_2\tau_1 \\ &=& (a \ c)(a \ d) (a \ c)(a \ b) \\ &=& \big\{(a \ c)(a \ d)\big\}\big\{ (a \ c)(a \ b)\big\} \\ &=& (a \ d \ c)(a \ b \ c) \end{eqnarray*} \[ \therefore \ (c \ d)(a \ b) = (a \ d \ c)(a \ b \ c) \]

以上により、全ての互換の積は3サイクル、または、3サイクルの積で表されることが分かった。ゆえに、${n \ge 3}$ の場合に全ての${A_n}$は3サイクルから生成される。