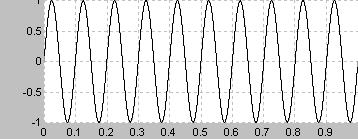
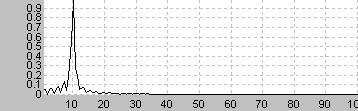
周波数特性の評価では、特定の周波数を最も大きなエネルギーを加えるため、周波数が限定される場合には有効
窓関数などの評価にも使いやすい
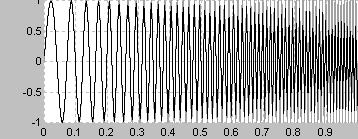
広範囲の周波数を短時間に効率的に加えられるが、特定の周波数のエネルギーは比較的小さくなる
人間の耳には高音側が間延びして聞こえやすい
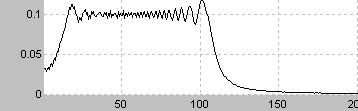
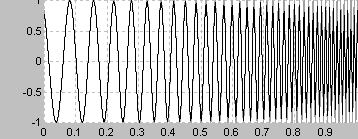
線形に比較すると低周波が強調される
人間の耳には比較的音が線形に変化して聞こえる
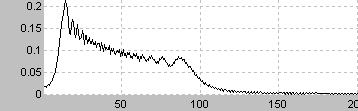
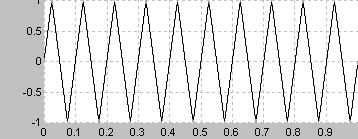
波形が直線で結ばれた三角形の波形となる
周波数領域では信号の周波数fの奇数倍の周波数すなわち(2n-1)fのみが含まれる
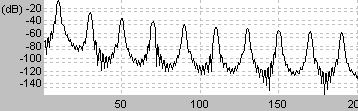
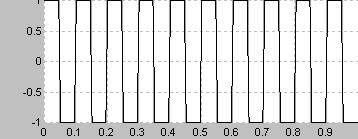
これにより波形を表示すると凸凹というかんじになり、矩形(長方形)に見える
これは非常に急激な過渡状態を繰り返すことになるため、過渡応答を評価する際にステップ応答とともに使うことができる
理論的には無限の周波数を含むため、伝達する中で信号のひずみを評価することができる
タイムストレッチ等の機能を評価するにも使われている
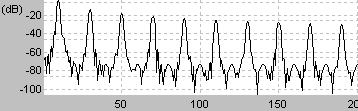
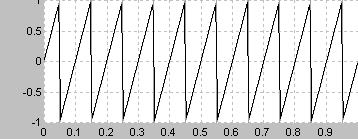
周波数領域では信号の周波数fの整数倍の周波数すなわちnfのみが含まれる
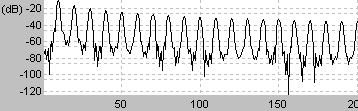
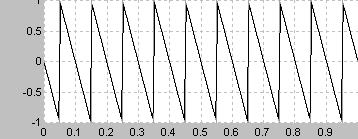
のこぎり波と同様に周波数領域では信号の周波数fの整数倍の周波数すなわちnfのみが含まれる
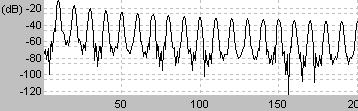
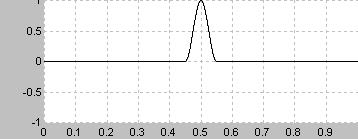
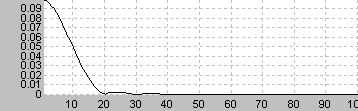
制御理論などででてくるインパルス関数は無限に短い時間幅しかない波だが、実験モード解析におけるインパルス波は比較的短い時間内の波になる
特徴は周波数領域では時間幅の逆数の周波数までフラットな特性を持つ
この周波数までは一定の強さの振動を加えることができる
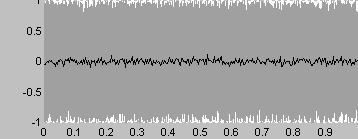
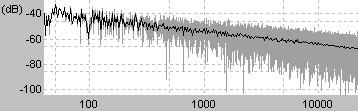
特に全周波数にわたってエネルギーが均一なノイズ
結果的にFFTにより周波数領域に変換すると平らになる
FFTを普通にかけるには一番素直なのであるが耳で聞くには高音が強調された音に聞こえる
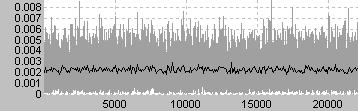
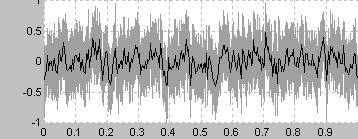
周波数が2倍(つまり1オクターブ上)になると振幅が1/2倍になるという周波数特性をもったノイズ
人間の耳にはさまざまな音が均一に混ざっているように聞こえる
そのためオーディオ等の耳による調整に一般的に用いられる