(式－１) 台形断面の等流計算
Ｍａｎｎｉｎｇの公式
開水路の等流計算には、次のマニングの公式がよく用いられる。
(式－１)
（式－２） 補足 （上底＋下底）×高さ÷２ で上底＝
として整理する。
（式－３） 
（式－４）
（式－５） 又は、 
（式－６）
ここで、各記号は次のことを示している。
Ｑ：流量
Ｖ：平均流速
ｎ：粗度係数（水路壁面、底面の粗さを示す値で、水路の材質や状態により異なる。）
R：径深（水理学的平均水深とも言う。 流積を潤辺で割ったもの）
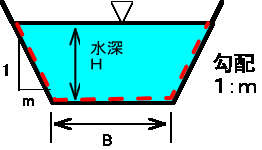
Ｓ：潤辺（水路断面において、水が周囲の壁や底と接する長さ。）下の図の---の長さ。
Ａ：水路における流水の断面積
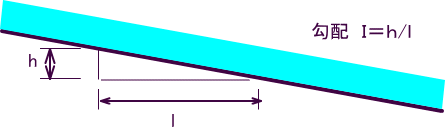
Ｉ：動水勾配 ｈｆ/Ｌ （ｈｆ：エネルギー損失 Ｌ：水路延長）
但し、等流では、動水勾配＝水面勾配＝水路床勾配であるので、計算には水路床勾配を用いることが多い。
課題 1 台形断面水路の流速と流量を求める。
 |
 |
計算の手順
手順１ 計算に必要な、水路の断面形状のデーターと勾配のデーターを整理する。
水路の幅と高さ、法面の勾配、水路底面の勾配（縦断図から、高さ（）：長さ（ｌ）の比を求める。） を求める。
手順２ 水路の材質や表面の凹凸、水路内の草など植生の状況などから、設計基準などの表を参考に粗度係数を求める。
手順３ データーがそろったところで、まず、流水の面積（流積）を求める。→（式－２）
手順４ 潤辺を求めよう。潤辺は、上の断面図の赤線部分となる。 →（式－４）
手順５ 水路の勾配を求よう。予め手順１で勾配が直接与えられているときは、その値を用いる。
水路勾配 Ｉ＝ｈ/ｌ または、設計で与えられた勾配を求める。
（注意 設計で勾配が例えば１：２００のように与えられた場合は、
ｈ：ｌ＝１：２００の意味なので、勾配Ｉ＝１／２００＝0.005と計算する。）
手順６ 面積（流積）と潤辺から径深（Ｒ）を求める。→（式－３）
手順７ 手順１～６までで求めた値を使って、式－５または式－６から、まず流速（Ｖ）を求める。
手順８ 求めた流速に流積をかけて、式－１から流量（Ｑ）を求める。
計算。
計算結果
課題 ２ 決められた水深で、必要な流量を流すために設定しなければならない水路の勾配を求める。
計算の手順
手順１ 計算に必要な、水路の断面形状のデーターと勾配のデーターを整理する。
水路の幅と高さ、法面の勾配、設計で流す流量を求める。
手順２ 水路の材質や表面の凹凸、水路内の草など植生の状況などから、設計基準などの表を参考に粗度係数を求める。
手順３ データーがそろったところで、まず、流水の面積（流積）を求める。→（式－２）
手順４ 潤辺を求めよう。潤辺は、上の断面図の赤線部分となる。 →（式－４）
手順５ 面積（流積）と潤辺から径深（Ｒ）を求める。→（式－３）
手順６ 勾配を求めるため、式－１及び式－５を勾配Ｉ について整理する。
したがって、一番左の式と一番右の式を整理して
から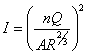 
が求められる。
手順７ 求めた勾配（Ｉ）の値を使って、式－５または式－６から、流速（Ｖ）も求める。
計算
計算結果
注意 水路の勾配は普通 ［１；ｍ］または［ｍ分の１］の形で表されるので、ｍ＝１/Ｉ から ｍを求める。
課題 ３ 台形断面水路の等流水深を求める。
この問題を解くためには、方程式の数値解法の知識を使う。
Ｍａｎｎｉｎｇの公式を用いると台形水路の水深を求める流量公式は、次のような高次方程式になる。
を変形して 
（式－3－1）
ここで、面積（Ａ）と径深（Ｒ）をＨの関数で表すと、
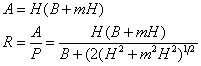
これを（式－３－１）に代入し
と表現すると
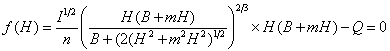
を両辺にかけて整理すると、
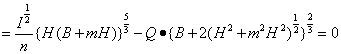（式－３－２）
となります。
この方程式を解くため、ここでは数値解法として代表的な「ニュートン・ラフソン法」を用いて答えを導いている。
ニュートン・ラフソンの公式は、
となります。 （式-３－３）
ここで、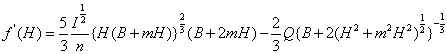
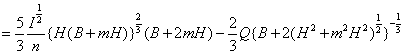
（式－３－４）となります。
ニュートン・ラフソンの公式に（式-３－２）・（式－３－４）を適用して、初期値（χ0）を適当に仮定して、χ１を求める。
このχ１をχ0として次のχ１を求め、χ0とχ１の差が無視できるほど小さくなるまで計算を繰り返しす。
例題
計算条件 流量 流量 ５ｍ３/ｓ 水路底幅 ４ｍ 法面勾配 １：０．５ 水路勾配 １／１０００ 粗度係数 ０．０１５
計算結果は、次のとおり７回の試算で、 Ｈ＝0.769ｍ に収束した。
| 計算回数 | χ0 |  |
 |
χ１ |
| 1 | 4.0000 | 393.4146 | 230.7030 | 2.2947 |
| 2 | 2.2947 | 107.3073 | 111.1459 | 1.3293 |
| 3 | 1.3293 | 25.8696 | 59.2968 | 0.8930 |
| 4 | 0.8930 | 4.4859 | 39.0065 | 0.7780 |
| 5 | 0.7780 | 0.2942 | 33.9044 | 0.7693 |
| 6 | 0.7693 | 0.0017 | 33.5227 | 0.7692 |
| 7 | 0.7692 | 0.0000 | 33.5206 | 0.7692 |
計算
