Chapter Seventeen

第17話

四則演算ができあがったので、今度は人間が理解しやすい１０進数との変換VIを作ろう。あまりぱっとしたアイデアが浮かばないので、地道に変換を行うことにする。
１０進数のストリングからU32nへの変換は、たとえば3892 = 2×1 ＋9×10 ＋8×100 ＋3×1000の計算を行う要領でできる。

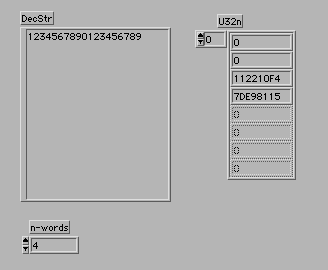
手順は以下の繰り返しだが、ダイアグラムを見てもらうと分かりやすいと思う。
(1)１０進数のストリングを下から１個切り取ってU32n数値に変換する。
(2)切り取った部分の桁数だけU32nでのA(Hex)を繰り返しかけたものに、(1)でつくったU32nをかける。
(3)0に初期化したU32nにたしこむ。

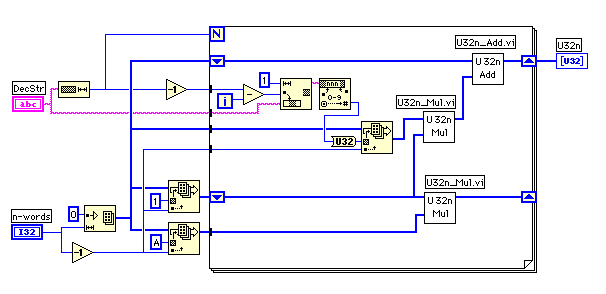
U32nから１０進数のストリングへの変換は、少し分かりにくいかもしれない。


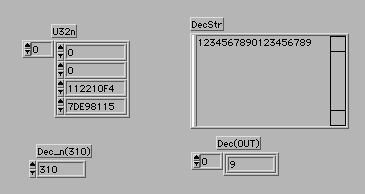
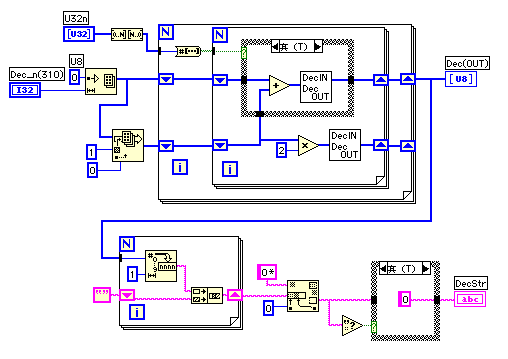
ダイアグラムに訳の分からないDecInDecOutというサブVIが入っているが、とりあえず無視してDec(OUT)という出力に注目しよう。２重ループはU32nというU32の１次元配列をDec(OUT)というU8の１次元配列に変換するものだ。Dec(OUT)は１０進数の位ごとの数値（０～９）で配列の０番目が１の位になっている。Dec(OUT)を一つづつストリングに変換して、先頭に連なる０を取り除くと目的の変換が終了する。
DecInDecOutは、ある要素の数値(0～255)の一桁目のみを残してその上の桁を次の要素にたし込むことで１０進数の桁上げをするVIだ。


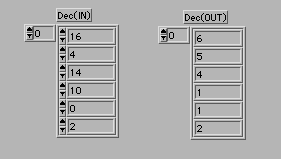
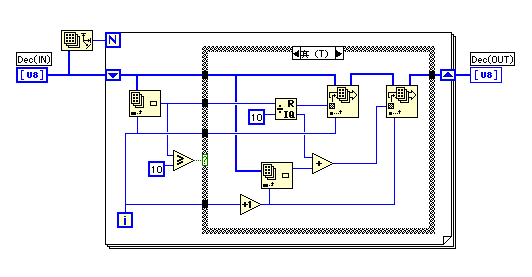
U32nから１０進数のストリングへの変換のための２重ループの説明に戻ろう。
２重ループの中では、U8配列表現で２のべき乗を計算し、U32の要素をブーリアンに変換して１のときに加算する。それぞれの処理の後でDecInDecOutを使って桁上げ処理を行う。
もっと良い方法が有りそうなもんだが、意見があったらよろしく！
See you! Nigel Yamaguchi 戻る