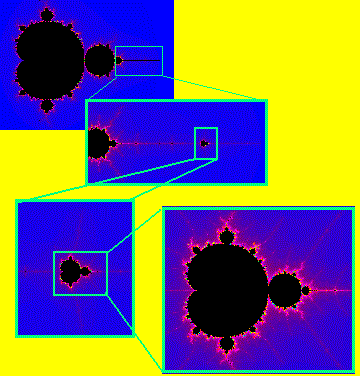
よくある描き方は、マンデルブロー集合自体を黒色で描き、まわりの発散部分を∞に
なる速さに応じて色で塗り分ける方法です。すると黒いマンデルブロー集合の周辺に色
鮮やかな光景の図形を描くことができます。この様に描いた図形は、マンデルブロー集
合がもつ自己相似性、つまり至るところの細部が全体図形の小さなコピーになるという
フラクタル構造を示します。
　フラクタル（fractal）は、７０年代にマンデルブロー(B.B.Mandelbrot)により導入
された言葉です。彼の著書 "The Fractal Geometry of Nature"が１９８３年に出版
されると、広く一般に知られるようになりました。当時と比べると、現在のコンピュー
タの性能は遥かに向上しました。高性能になったコンピュータを活かして、この様な自
己相似図形を手軽に愉しみましょう。

　以下では、図形の一部をどんどん拡大して行くプログラムを作ります。次の図は、作
成したプログラムの実行の様子を一枚の画像に編集したものです。４倍毎に拡大してい
ます。この拡大操作を１０回繰り返すと約１００万倍の倍率を描くことになります。




　マンデルブロー集合は点列が、n → ∞ で有界となる集合です。コンピュータでは無
限大の繰り返し計算なんてできないので、繰り返し計算の上限値を決めて、前ページの
判定条件で上限値まで満たされればマンデルブロー集合と見なします。また途中で発散
となれば、そのときの繰り返し数に対応した色を付け光景を描きます。
　次の関数は、繰り返しの上限値 NMAX まで計算し、マンデルブロー集合の点では 0 
を返し、発散するときは繰り返し数を返します。

int mandelbrot(double a, double b)
{
    double x = 0.0, y = 0.0, x1, y1;
    for(int n=1; n < NMAX; n++){
        x1 = x * x - y * y -a;
        y1= 2.0 * x * y - b;
        if( x1*x1 + y1*y1 > 4.0 ) return n; // 発散
        x=x1; y=y1;   // 点列の更新
    }

    return 0;
}

　この関数を、パラメータλの各点（ピクセル単位）について、繰り返し呼び出しその
返却値に対応する色で点を打ちます。

　ここでは、Windows 95/98 用のグラフィックス・クラスライブラリ GLIBW32 のメン
バ関数 GRAPH::wmouse() を使って、マウス左ボタンが押された座標値(a0, b0)を中心
とする拡大図を再描画するプログラムを書きます。またマンデルブロー集合背景の光景
を２５６色で描きます。

　main() 関数を擬似コードで書くと次の様になります。

    中心座標(a0, b0)と区間幅vsの初期値を設定

    グラフィックスの初期化

    do{
        画面消去

        座標(a0, b0)を中心に区間±vsの正方形領域に
       グラフィックス・ウィンドウを設定する

        for( a0 - vs <= a <= a0 + vs の区間){
            各a（λの実数部）に対して

            for( b0 - vs <= b <= b0 + vs  の区間){
                各b（λの虚数部）に対して

                int n = mandelbrot(a,b);
                if( n ) 位置(a,b)にｎ番の色で点を打つ;
            }
        }
        vs /= factor; // 区間幅を縮小

    }while(g.wmouse(a0,b0) != 1);// 右ボタンが押されるまで

    グラフィックスの終了処理

}

次の図は、約１００万倍に拡大した小マンデルブロー集合です。



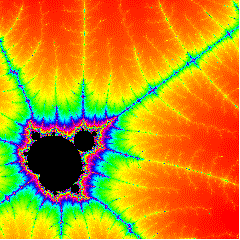次の図は、約１億倍に拡大したものです。

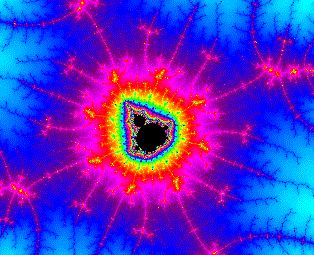
実行ファイルとソースファイルのダウンロードはこちらです、

マンデルブロー集合 実行ファイルとソース・ファイル Windows 95/ 98上で動作します。

ダウンロード 　　mandelbt.lzh (26KB)

　* このソフトウェアは、SYMANTEC. NORTON AntiVirus 5.0 でウィルス検査を 
　　行っています。 
　* ファイルは吉崎栄泰氏による LHA (Copyright(c)1988-92 H.Yoshizaki)を 
　　使って圧縮しています。 

| 目次| 前のページ |

Copyright(c) 2000 Yamada,K