演算子の機能を確認するために簡単なプログラムを書いてみます。ここで利用するベ クトルと行列のクラス・インターフェースはこちらをご覧ください。 これらは、ヘッダファイル( matrix17.h )、関数定義プログラム( matrix17.cpp ) にまとめてあります。
3.9.1 ベクトルと行列の演算
次のプログラムは、ベクトル演算子の使用法を示しています。
// lst03_19.cpp
// ベクトルの演算をテストする
//matrix17.cppと一緒にコンパイルする
#include <iostream.h>
#include "matrix17.h"
int main()
{
Vector x(4), y(4);
for(int i = 0; i < x.getSize(); i++){
y[i] = 0.2 * (i+1);
y[i] = 0.1 * (i+1);
}
//x, yの内容をプリントする
cout << "x: " << x << "y: " << y << endl;
//ベクトルの和
cout << " x + y : " << ( x + y );
//ベクトルの差
cout << " x - y : " << ( x - y ) << endl;
// ベクトルの内積
cout << " x * y = " << x * y << endl << endl;
// 等値演算子
if( x == ( 2 * y ) ) cout << "x と ( 2 * y ) は等しい。\n" << endl;
// -x
cout << "-x: " << -x << endl;
// ベクトルを3倍する
cout << "3.0 * x : " << 3.0 * x;
cout << "y * 3.0 : " << y * 3.0 << endl;
y *= 2.0;
cout << " y *= 2.0 の結果:" << endl << y;
x /= 2.0;
cout << " x /= 2.0 の結果:" << endl << x << endl;
// ベクトルを規格化する
cout << "xを規格化: " << x.normalize();
cout << "xのノルム: " << x.norm() << endl;
return 0;
}
|
[実行結果] ソースプログラム ( lst03_19.cpp )
x: 2.000000e-01 4.000000e-01 6.000000e-01 8.000000e-01 y: 1.000000e-01 2.000000e-01 3.000000e-01 4.000000e-01 x + y : 3.000000e-01 6.000000e-01 9.000000e-01 1.200000e+00 x - y : 1.000000e-01 2.000000e-01 3.000000e-01 4.000000e-01 x * y = 6.000000e-01 x と ( 2 * y ) は等しい。 -x: -2.000000e-01 -4.000000e-01 -6.000000e-01 -8.000000e-01 3.0 * x : 6.000000e-01 1.200000e+00 1.800000e+00 2.400000e+00 y * 3.0 : 3.000000e-01 6.000000e-01 9.000000e-01 1.200000e+00 y *= 2.0 の結果: 2.000000e-01 4.000000e-01 6.000000e-01 8.000000e-01 x /= 2.0 の結果: 1.000000e-01 2.000000e-01 3.000000e-01 4.000000e-01 xを規格化: 1.825742e-01 3.651484e-01 5.477226e-01 7.302967e-01 xのノルム: 1.000000e+00 |
同じ次元の2つのベクトル・オブジェクトに対する算術演算には、次の3つがあり、 x + y; // 和 x - y; // 差 x * y; // 内積 またベクトル・オブジェクトと実数(浮動小数点数)との演算には、 x * 3.0; // 実数倍 3.0 * x; // 実数倍 x / 2.0; // 割り算 -x; // マイナスのベクトル がサポートされています。これらはオブジェクト自体は変更されません。オブジェクト が変更される算術演算には、 x += y; // x = x + y x -= y; // x = x - y x *= 2.0 // x = 2 * x x /= 2.0 // x = x / 2 が利用できます。 次のプログラムは、行列の演算子の使い方を示します。
// lst03_20.cpp
// 行列の和・差・積
//matrix17.cppと一緒にコンパイルする
#include <iostream.h>
#include <iomanip.h>
#include "matrix17.h"
int main()
{
Matrix a(3,3), b(3,3);
int i,j;
for(i = 0; i < a.getRow(); i++)
for(j = 0; j < a.getCol(); j++){
a[i][j] = 2.0 * (i+1) + 0.1*(j+1);
b[i][j] = (i+1) + 0.2*(j+1);
}
cout << "行列 a: \n" << a << endl;
cout << "行列 b: \n" << b << endl;
cout << "行列の和 a + b: " << endl << ( a + b ) << endl;
cout << "行列の差 a - b: " << endl << ( a - b ) << endl;
a.setSize(2,3);
b.setSize(3,2);
for(i = 0; i < a.getRow(); i++)
for(j = 0; j < a.getCol(); j++)
a[i][j] = i+j+1;
cout << "行列 a: \n" << a << endl;
for(i = 0; i < b.getRow(); i++)
for(j = 0; j < b.getCol(); j++)
b[i][j] = i+j+1;
cout << "行列 b: \n" << b << endl;
Matrix c = a * b;
cout << "行列の積 c = a * b: \n" << c << endl;
c.setSize(3,3);
c = b * a;
cout << "行列の積 c = b * a: \n" << c << endl;
return 0;
} |
行列 a: 2.100000e+00 2.200000e+00 2.300000e+00 4.100000e+00 4.200000e+00 4.300000e+00 6.100000e+00 6.200000e+00 6.300000e+00 行列 b: 1.200000e+00 1.400000e+00 1.600000e+00 2.200000e+00 2.400000e+00 2.600000e+00 3.200000e+00 3.400000e+00 3.600000e+00 行列の和 a + b: 3.300000e+00 3.600000e+00 3.900000e+00 6.300000e+00 6.600000e+00 6.900000e+00 9.300000e+00 9.600000e+00 9.900000e+00 行列の差 a - b: 9.000000e-01 8.000000e-01 7.000000e-01 1.900000e+00 1.800000e+00 1.700000e+00 2.900000e+00 2.800000e+00 2.700000e+00 行列 a: 1.000000e+00 2.000000e+00 3.000000e+00 2.000000e+00 3.000000e+00 4.000000e+00 行列 b: 1.000000e+00 2.000000e+00 2.000000e+00 3.000000e+00 3.000000e+00 4.000000e+00 行列の積 c = a * b: 1.400000e+01 2.000000e+01 2.000000e+01 2.900000e+01 行列の積 c = b * a: 5.000000e+00 8.000000e+00 1.100000e+01 8.000000e+00 1.300000e+01 1.800000e+01 1.100000e+01 1.800000e+01 2.500000e+01 |
行列オブジェクト同士の算術演算は和と差 a + b; a - b; があり、これらは行数と列数が等しい2つの行列に対して定義されています。また、 (L×M)の行列aと(M×N)の行列bの積は c = a * b; と表現できて、演算結果を代入した行列cは(L×N)行列でなければなりません。間 違った型同士の演算を行うと、呼び出された演算子関数はエラーメッセージを表示して プログラムを終了させます。 この様な単純な機能確認プログラムでは退屈なので、少しばかり教養的な話題を取り 上げます。以下では、行列とベクトルの積および行列と行列の積を使ったプログラムを 扱います。
3.9.2 固有値方程式
n行n列の正方行列Aに対して、次の方程式を固有値方程式といいます。
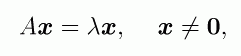
ここで、定数λを行列Aの固有値、n次元ベクトルxを固有値λに属する固有ベクトル と呼び、これらを求めることを固有値方程式を解くといいます。この式は行列に固有ベ クトルを掛けると、自身に比例するベクトル、すなわち固有ベクトルのスカラー倍(固 有値倍)が得られることを意味します。 この意味を具体的に見ることにしましょう。例として、次の2行2列の行列
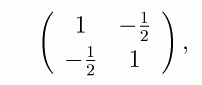
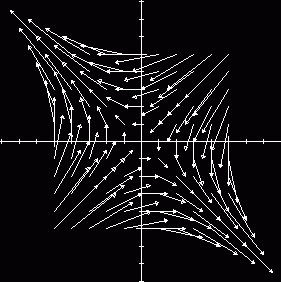
を取り上げます。この行列に、ベクトル (x,y)を掛けると (x -0.5*y, -0.5*x + y)が 得られます。これを、平面上の点 (x,y)が行列によって点 (x -0.5*y, -0.5*x + y)に 移される写像と見なすことができます。色々な点に対して、元の点から移った点へ矢印 を引いて描いてみると、次のような図形が得られます。
 ソースプログラム
( lst03_21.cpp )
ソースプログラム
( lst03_21.cpp )
図を見ると矢印の変化には、2つの流れがあります。引き伸ばしと圧縮です。引き伸ば しは、直線「 y = -x 」に沿って起こり、この直線の近くの点はこの直線に沿って原点 から引き離されています。一方、圧縮は直線「 y = x」に沿って、原点に向かって押し 込もうとしています。 すべての点は、これら引き伸ばしと圧縮の2つの作用の組み合わせで移動しています。 そして、この2つの直線上の点はすべてその直線上に移ります。すると、点(1,1)は 直線「 y = x」上の点であり、また点(1, −1)は直線「 y = -x 」上の点ですから、
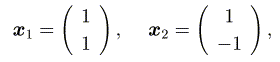
をそれぞれ行列に掛けたものは、
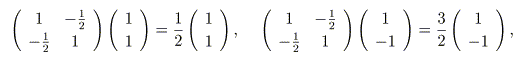
となります。これはまさに固有値方程式です。この行列の固有値は、1/2 と 3/2で、 それぞれに属する固有ベクトルは(1、1)と(1、−1)となります。 つまり固有ベクトルとは、「引き伸ばしと圧縮」をする方向のベクトルという意味を 持ちます。そして、その伸縮の比率が固有値です。
この性質を利用することで、固有値と固有ベクトルを求めることができます。アイデ アは、こうです。あるベクトルから初めて、このベクトルを繰り返し行列に掛けて行く と得られるベクトルは固有ベクトルの1つに近づいて行くであろう。これは、べき乗法 といわれるもので、次のように述べられます。

べき乗法の証明はこちらにあります。
この方法は、絶対値最大の固有値と固有ベクトルしか求めることができません。これ は決して実用的とはいえませんが、行列とベクトルの掛け算を繰り返すだけの簡単なも のであり、行列の面白い性質を示しています。例題を1つ考えましょう。次の行列
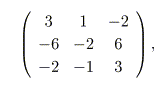
は2と1(重解)の2つの固有値を持ちます。べき乗法を使って大きい方の固有値とそ の固有ベクトルを求めてみましょう。
// lst03_22.cpp
// べき乗法 (Power method)
//matrix17.cppと一緒にコンパイルする
#include <iostream.h>
#include "matrix17.h"
const int MAX_ITERATION = 100; // 繰り返しの上限
int power(const Matrix &, Vector &, double &);
int main()
{
cout << "べき乗法 (Power method)" << endl << endl;
// 行列
// この行列の固有値は:2,1(重解)
double mat[3][3] = {{ 3.0, 1.0, -2.0},
{ -6.0, -2.0, 6.0},
{ -2.0, -1.0, 3.0}};
Matrix a(3,3);// Matrixクラスのオブジェクトを生成する
// 行列の読み込み
for(int i = 0; i < a.getRow(); i++)
for(int j = 0; j < a.getCol(); j++)
a[i][j] = mat[i][j];
cout << "行列:" << endl << a << endl;
// べき乗法
double lambda;// 最大固有値
Vector v(3); // 固有ベクトル
int status = power(a, v, lambda);
if(!status){
cout << endl << "最大固有値:" << lambda << endl;
cout << "固有ベクトル:" << v << endl;
}
return 0;
}
/*
* ========================
* べき乗法 (Power method)
* ========================
* (入力)
* a:Matrix型の行列(変更されない)
* v:Vector型の求める固有ベクトル
* λ:求める絶対値が最大の固有値
* (出力)
* v:固有ベクトル(ベクトルvに上書きして返す)
* λ:λに上書きして返す
* (戻り値)
* 0:成功
* 1:行列とベクトルの型が一致しない
* 2:初期ベクトルが見つからない
* 3:固有ベクトルがヌルベクトルになった
* 4:収束しなかった
*/
int power(const Matrix &a, Vector &v, double &lambda)
{
// 行列とベクトルの型チェック
int size = v.getSize();
if( ( size != a.getRow() ) || ( size != a.getCol()) ){
cout << "行列とベクトルの型が一致しません。" << endl;
return (1);
}
// 初期ベクトルの設定
Vector v_old(size);// ベクトルはゼロで初期化
for(int i = 0; i < size; i++){
v_old[i] = 1.0;
v = a * v_old;
if( v.norm() > NEARLY_ZERO ) break;
v_old[i] = 0.0;
}
if( v.norm() < 1.0) return (2);// 初期ベクトルが見つからない
int k = 1;
while(k < MAX_ITERATION){
v = a * v_old; // 固有ベクトル
lambda = v * v_old;// 最大固有値
if( v.norm() < NEARLY_ZERO ) return (3); // ヌルベクトル
v.normalize(); // 固有ベクトルを規格化
if( v == v_old ){
cout << "繰り返し数: " << k << endl;
return (0); // 正常終了(収束した)
}
v_old = v;
++k;
}
return (4); // 収束しない
}
|
べき乗法 (Power method)
行列:
3.000000e+00 1.000000e+00 -2.000000e+00
-6.000000e+00 -2.000000e+00 6.000000e+00
-2.000000e+00 -1.000000e+00 3.000000e+00
繰り返し数: 50
最大固有値:2.000000e+00
固有ベクトル: 3.015114e-01 -9.045340e-01 -3.015113e-01 |
アルゴリズムの骨格は簡単で、行列とベクトルの掛け算を繰り返し、ベクトルが一定の
値に収束するまで続けます。擬似コードは、
int k = 1; // 繰り返しの数
while(k < MAX_ITERATION){
v = a * v_old; // 固有ベクトルの近似値
最大固有値の近似値を計算
ベクトルvを規格化する
if( v == v_old ) 終了
v_old = v; // 更新
++k;
}
となります。
このプログラムでは50回繰り返していますが、収束の判定条件を緩めて、
if( v == v_old )
の代わりに、ベクトルの差のノルムがある値(たとえば 1.E-8)以下になるまで繰り返
すようにすると、収束は速くなります。つまり、
Vector dv = v - v_old;// ベクトルの差
if( dv.norm() < 1.E-8 )
で置き換えます(この場合、24回で求まる)。
3.9.4 有限 Markov連鎖
最後に、行列の掛け算を繰り返す例を取り上げます。サイコロを繰り返し振る場合の ように時間と共に変化する確率現象は確率過程(stchastic process)と呼ばれます。 わたしたちの周囲には、ランダムな現象が引き続いて起こるという例は数多くみられま す。確率過程は、この様な一連の現象の系列を扱う数学モデルで、自然科学、工学や経 済学などの広い分野で現象の解析に使われています。 とくに確率変数が有限の数で構成され (例えばサイコロの場合では1〜6の目の数) て、しかも時間の系列が離散的(つまり1回目、2回目...と数えられる)である確率 過程を有限マルコフ連鎖といいます。 有限マルコフ連鎖をなすシステムは、行列を使って記述することができます。これを 推移確率行列と呼び、次のような正方行列で表されます。
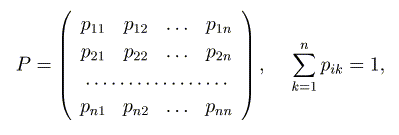
この行列は、n個の確率変数を持ち、各行ベクトルは状態間の推移確率を表します。 i行j列の要素は、現在の状態iから、次の時刻に状態jに移行する条件付き確率を 示します。従って、各行の値の合計は1(全確率)になります。このとき繰り返して起 こる確率現象は、この行列の掛け算を繰り返したものを調べることで、行き着く先での 状態の確率が計算できます。例えば次の行列は、推移確率行列の1つです。
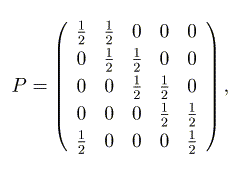
この推移確率行列の掛け算の極限値は、初等的な計算から簡単に求めることができて
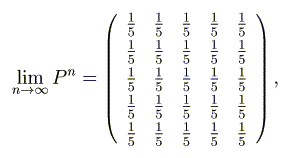
となります。プログラムで、この繰り返し掛け算を計算してみましょう。
// lst03_23.cpp
// 確率過程(有限 Markov連鎖)
//matrix17.cppと一緒にコンパイルする
#include <iostream.h>
#include "matrix17.h"
const int MAX = 10000; // 上限
int main()
{
// 推移確率行列
double mat[5][5] = {{ 0.5, 0.5, 0.0, 0.0, 0.0},
{ 0.0, 0.5, 0.5, 0.0, 0.0},
{ 0.0, 0.0, 0.5, 0.5, 0.0},
{ 0.0, 0.0, 0.0, 0.5, 0.5},
{ 0.5, 0.0, 0.0, 0.0, 0.5}};
Matrix a(5,5);// Matrixクラスのオブジェクトを生成する
// 行列の読み込み
for(int i = 0; i < a.getRow(); i++)
for(int j = 0; j < a.getCol(); j++)
a[i][j] = mat[i][j];
cout << "推移確率行列:" << endl << a << endl;
int n = 1; // 試行数
Matrix b = a;
while( n < MAX ){
++n;
Matrix c = b;
b *= a;
if( b == c ) break; // 収束
}
cout << n << "次推移確率行列:" << endl << b << endl;
return 0;
}
|
推移確率行列:
5.000000e-01 5.000000e-01 0.000000e+00 0.000000e+00 0.000000e+00
0.000000e+00 5.000000e-01 5.000000e-01 0.000000e+00 0.000000e+00
0.000000e+00 0.000000e+00 5.000000e-01 5.000000e-01 0.000000e+00
0.000000e+00 0.000000e+00 0.000000e+00 5.000000e-01 5.000000e-01
5.000000e-01 0.000000e+00 0.000000e+00 0.000000e+00 5.000000e-01
169次推移確率行列:
2.000000e-01 2.000000e-01 2.000000e-01 2.000000e-01 2.000000e-01
2.000000e-01 2.000000e-01 2.000000e-01 2.000000e-01 2.000000e-01
2.000000e-01 2.000000e-01 2.000000e-01 2.000000e-01 2.000000e-01
2.000000e-01 2.000000e-01 2.000000e-01 2.000000e-01 2.000000e-01
2.000000e-01 2.000000e-01 2.000000e-01 2.000000e-01 2.000000e-01 |
この様に、演算子を多重定義することで、クラスを利用するプログラムは直感的で簡単 になります。 次のページでは、ベクトルと行列のクラスの効率について検討します。
| 目次 | 前のページ | 次のページ | ページの先頭 |
Copyright(c) 1999 Yamada, K