前回に続きデータの入れ物つまりデータ構造を扱います。ここでは行列ライブラリを 設計します。行列は行(row)と列(column)に値を配置した表の構造をしていますから、 ２次元配列で表現できます。 ２次元配列を使った行列ライブラリを設計する過程で配列とポインタとの密接な関係 が鮮明になってきます。その知識は連立方程式や固有値問題などの行列計算に限らず、 エディタなどの文書処理ソフトウェアの作成にも応用することができます。 以下（ライブラリの設計（１））ではまず、Ｃ++で手続き型（非オブジェクト志向） のライブラリを構築します。これは本質的にはＣ言語プログラミングです。その後設計 （２）でオブジェクト指向のクラス・ライブラリを構築します。これにより強力で柔軟 性のある関数ライブラリをつくることができます。関連する基本的概念を整理しながら、 ゆっくり進みます。2.1 配列
2.1.1 配列の宣言 配列は同一型のデータを格納するための連続したメモリ領域です。配列の１つ１つのデ ータ項目を要素、配列の要素数を次元といいます。配列は次のような宣言でメモリ内に確 保されます。 int a[3]; // 宣言 この配列ａは３個のint型のデータ（要素）があり、それぞれの要素は int型の別々の変 数a[0],a[1],a[2]として読み書きすることができます。配列の要素の番号（添字）は０ （ゼロ）から始まり（次元−１）で終わります。なぜそうなのかは、後で行うポインタと の関係についての議論から明らかになります。 宣言時に、中括弧｛｝を使って初期値を並べて与えることで要素を初期化することができ ます。 int a[3] = { 5, 2, 9 }; // a[0]は５、a[1]は２、a[2]は９に初期化 また、初期値の数が配列要素の数より少ない場合は、残りの要素は０に初期化されます。 従って次の場合 int a[10] = {0}; は１０個の配列要素の値はすべて０で初期化されます。初期値リストを付けた配列宣言で は配列のサイズを省略できます。 int a[] = { 1, 2, 3, 4, 5}; は、５個の要素の配列を確保します。しかし、次の宣言 int a[3] = { 1, 2, 3, 4}; // エラー は、３要素しかない配列に４個の初期値を指定しているために、構文エラーになります。 ★配列を使った例題
2.1.2 ２次元配列 ２次元配列は行(row)と列(column)に値を配置した表の構造をしています。その宣言は ２組の角括弧（大括弧）[ ]を使って行と列のサイズを指定します。 int mat[4][5]; は行のサイズが４、列のサイズが５の int型の配列名 mat を意味します。 mat[i][j] はｉ行ｊ列目の要素でｉ、ｊの範囲は０≦ｉ≦３，０≦ｊ≦４となります。プログラム 例を挙げます。
// matrix01.cpp
// ４×５行列を２元配列で表す
// 行列の初期化
#include <iostream.h>
int main()
{
const int ROW = 4; //行の次元
const int COL = 5; //列の次元
int mat[][COL] = { {11,12,13,14,15},
{21,22,23,24,25},
{31,32,33,34,35},
{41,42,43,44,45} };
cout << "行列の表示\n";
for(int i = 0; i < ROW; i++){
for(int j = 0; j < COL; j++)
cout << " " << mat[i][j];
cout << endl; //行の終わりに改行
}
return 0;
}
|
行列の表示 11 12 13 14 15 21 22 23 24 25 31 32 33 34 35 41 42 43 44 45 |
2.1.3 アドレス演算子 配列がメモリ内でどのように配置されるかを見ます。変数やデータ型の記憶領域のバイ ト数は sizeof 演算子で知ることができます。 sizeof 単項式 sizeof( 型 ) は使用されるメモリ領域をバイト数で返します。 アドレスはメモリ内の位置（番地）をバイト単位で表したものです。アドレスを知るに はアドレス演算子＆を使います。アドレス演算子は、アドレスを返す単項演算子で、変数 の前にアンパーサンド（＆）を付けます。 int x = 6; cout << "ｘのアドレスは：" << &x << endl; は変数ｘの先頭位置のアドレスを画面に表示します。int型が４バイトとするとそのアド レスから４バイト分の領域に変数ｘの領域が配置されていることを意味します。
// matrix02.cpp
// ３×４行列のメモリー領域
#include <iostream.h>
int main()
{
const int ROW = 3; //行の次元
const int COL = 4; //列の次元
int a[ROW][COL];
cout << "int型の３×４行列" << endl;
cout << "行列のサイズ： sizeof(a) = " << sizeof(a) << endl
<< "列のサイズ： sizeof(a[0]) = " << sizeof(a[0]) << endl
<< "要素のサイズ： sizeof(a[0][0])= " << sizeof(a[0][0])
<< endl << endl;
cout << "行列の先頭アドレス： &a[0][0] = " << &a[0][0] << endl;
cout << "（または (void *)a = " << (void *)a << " でもよい）" << endl;
for(int i = 0; i < ROW; i++){
cout << i+1 << " 行目のアドレス: &a[" << i << "] = "
<< &a[i] << endl;
for(int j = 0; j < COL; j++){
cout << " &a[" << i << "][" << j << "] = "
<< &a[i][j] << endl;
}
}
return 0;
} |
int型の３×４行列
行列のサイズ： sizeof(a) = 48
列のサイズ： sizeof(a[0]) = 16
要素のサイズ： sizeof(a[0][0])= 4
行列の先頭アドレス： &a[0][0] = 0x0063FDC8
（または (void *)a = 0x0063FDC8 でもよい）
1 行目のアドレス: &a[0] = 0x0063FDC8
&a[0][0] = 0x0063FDC8
&a[0][1] = 0x0063FDCC
&a[0][2] = 0x0063FDD0
&a[0][3] = 0x0063FDD4
2 行目のアドレス: &a[1] = 0x0063FDD8
&a[1][0] = 0x0063FDD8
&a[1][1] = 0x0063FDDC
&a[1][2] = 0x0063FDE0
&a[1][3] = 0x0063FDE4
3 行目のアドレス: &a[2] = 0x0063FDE8
&a[2][0] = 0x0063FDE8
&a[2][1] = 0x0063FDEC
&a[2][2] = 0x0063FDF0
&a[2][3] = 0x0063FDF4 |
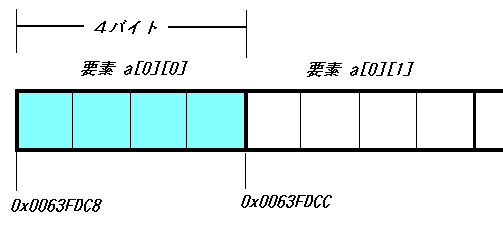プログラムの中で行列aに添字を１つだけ付けた表現a[0],a[1],a[2]があります。これ
らは各行の横の数の並びの１次元配列（つまり行ベクトル）を意味しています。つまり大
きさの関係は、
行列： a ----> ２次元配列
（横の並びの配列×行の数＝１６×３＝４８バイト）
行 ： a[0],a[1],a[2] ----> １次元配列
（横の並び＝int型×列の数＝４×４＝１６バイト）
要素：a[0][0],a[0][1],..----> 変数（int型＝４バイト）
で、
行列ａの先頭アドレス ＝ 第１行ａ[0]の先頭アドレス ＝ 要素ａ[0][0]の(先頭)アドレス,
第２行ａ[1]の先頭アドレス ＝ 要素ａ[1][0]の(先頭)アドレス,
第３行ａ[2]の先頭アドレス ＝ 要素ａ[2][0]の(先頭)アドレス,
となります。行列aは各行の配列を要素に持つ１次元配列であり、また各行はint型の１次
元配列というデータ構造になっています。数学のことばで言えば、１組の数を並べたものが
ベクトル。行ベクトル（横ベクトル）を縦に並べたものが行列。つまり行列はベクトルのベ
クトルです。
【演習問題2.2】この配列のメモリ内の位置の様子をできるだけ正確に図に描きなさい。
Copyright(c) 1999 Yamada,K