数列
index → 数学ハンドブック 公式集 (面積・体積・・) 関連:
![]() 数列
数列
ある規則に従って順に数を書き並べたものを数列という。
![]() 例:1,2,3,4,5,・・・・・
例:1,2,3,4,5,・・・・・
1,3,5,7,9,・・・・・
![]() 一般項
一般項
数列の第 n 項を表す式を、その数列の一般項という。
![]() 例:1,4,9,16,25,・・・・・
の一般項 anは、
例:1,4,9,16,25,・・・・・
の一般項 anは、
an = n2
![]() 等差数列
等差数列
数列で、各項と次の項との差が一定である数列。
![]() 例:1,3,5,7,9,・・・・・
公差 2
例:1,3,5,7,9,・・・・・
公差 2
3/4 , 2/4 , 1/4 , 0 , −1/4 , −2/4 ,・・・ 公差 −1/4
![]() 等差数列の一般項
等差数列の一般項
an = a + ( n−1)d
a:初項、 d:公差、 n:項数
例:a=3、 d=2の場合
3,5,7,9,11,・・・・・ 3 + ( n−1)×2 公差 2
an=3+(n−1)×2
![]() 等差数列の和
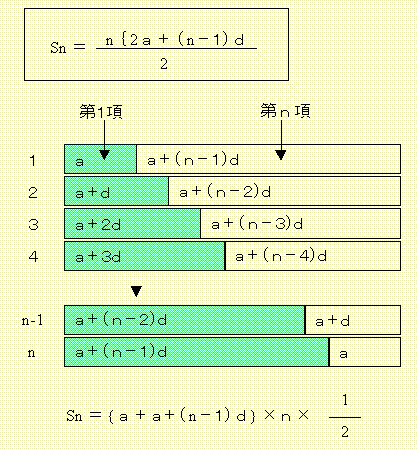
等差数列の和
初項 a から、公差 d の等差数列の初項から第 n 項までの和を Sn とすると
![]() 調和数列
調和数列
数列の各項の逆数を各項とする数列が等差数列となるとき、もとの数列を調和数列という。
![]() 例:1,1/3 ,1/5 ,1/7
,1/9 ,・・・・・
例:1,1/3 ,1/5 ,1/7
,1/9 ,・・・・・
一般項は、 an =1/ { a + ( n−1)d }
![]() 等比数列
等比数列
数列の初項につぎつぎ一定の数を掛けて作られる数列を等比数列という。
![]() 例:2,4,8,16,32,・・・・・
公比 2
例:2,4,8,16,32,・・・・・
公比 2
−125 , 25, −5 , 1 , −1/5 , 1/25 ,・・・ 公比 −1/5
![]() 等比数列の一般項an
= a r n-1
等比数列の一般項an
= a r n-1
an = a r n-1
a:初項、 r :公比、 n:項数
![]() 等比数列の和
等比数列の和
初項 a から、公比 r の等比数列の初項から第 n 項までの和を Sn とすると

![]() その他の数列
その他の数列
![]() 例:1,2,1,2,1,2,1,・・・・・
の一般項は
例:1,2,1,2,1,2,1,・・・・・
の一般項は
an = { 3+(−1)n } / 2
丶 jin 丶