ゆらぎの分析には、フーリエ変換という手法を用います。どのような複雑な変動も、単純なパターンの組み合わせから成り立っています。フーリエ解析は、簡単に言うと、複雑な変動を単純なパターンの組み合わせに分解して分析する手法です。

19世紀に活躍したフランスの数学者フーリエは、任意の波を、サイン波とコサイン波の組み合わせに変換するアルゴリズムを考案しました。逆に考えれば、サイン波とコサイン波の合成で複雑な音をつくれることになりますが、それを原理にしたものが、シンセサイザーです。（こちらもご覧ください。）

ゆらぎの分析では、フーリェ解析で分解した結果を各周波数ごとにグラフ化して分析を行います。周波数を水平軸、強さを垂直軸に示し、両軸とも対数をとり、両対数グラフの形式で表示します。

人間にとって心地の良い「1/fのゆらぎ」は、フーリエ変換したときに、分解された各周波数の成分が、その周波数の逆数に比例して大きくなるということを意味しています。つまり、1/fとは、周波数（frequency）の逆数のことなのです。

単純化して、3つの波とその合成波を見てみましょう。 下図には３つの波が示されていますが、周期の大きな波ほど、強い波になっています。

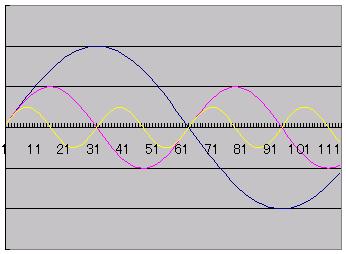上の３つの波を合成すると、下のようになります。逆に言うと、下の波をフーリエの手法で分解すると、上の３つの波が得られます。

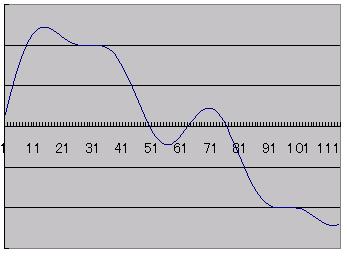周波数を水平軸、強さを垂直軸に示し、両軸とも対数をとり、両対数グラフの形式で表示すると、下図になります。

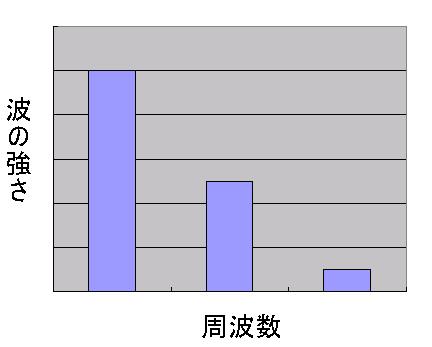３つの周波数の波に限定しない、通常の場合は、下のようなグラフになります。1/fのゆらぎ」では、下図のように、周期の長い波ほど大きな振幅に、周期の短い波ほど、小さな振幅になっています。

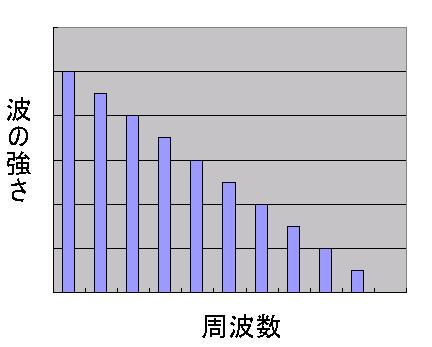これに対して、まったく繰り返しがなく、一様に分布するような乱数をフーリェ変換した場合は、下の図のようにになります。