Fourier transform is a useful method when you analyze fluctuation. No matter how complex the changes might be, they are made up of  combination of simple patterns. In other words, Fourier transform  is an analyzing  method to break complex changes down  into combination of simple patterns.

Fourier was a French mathematician of 19th and he introduced the algorithm that transforms any wave into combination of sine and cosine waves. To put it the other way around, it is possible to generate complex sound by the synthesis of sine and cosine waves. Synthesizers are based on this theory. (For further information, click here, but currently only Japanese page is available.)

In the fluctuation analysis, you will analyze by  the graph that shows the result of Fourier transformation at each frequency. The horizontal line indicates the frequencies while the vertical line indicates the strength. Both axis take logarithm, and the graph will be double logarithmic plot.

1/f Fluctuation means that when you perform Fourier transform, resolved components of each frequency gets bigger in proportion to the reciprocal number of the frequency. In other words, "1/f " is a reciprocal number of frequency.

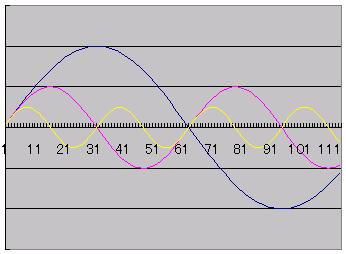
To put it simple, let us look into the three waves and their synthesized wave. You can see three waves in the figure below. The bigger the cycle of the wave is, the stronger the wave becomes.

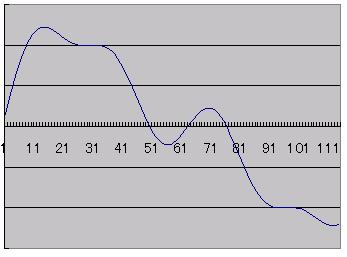
If you synthesize the three waves above, you will see the wave below. To put it the other way around, if you resolve the following wave by the Fourier's method, you will get the three waves above.

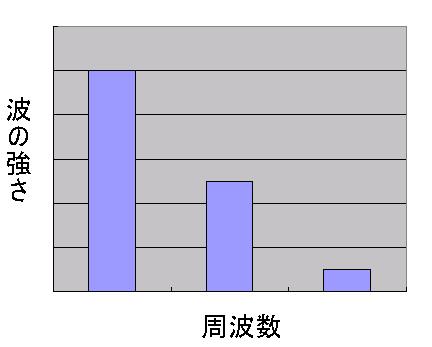
The chart below is a double logarithmic plot. The horizontal line indicates frequency, vertical line indicates wave strength, and both axis take logarithm.

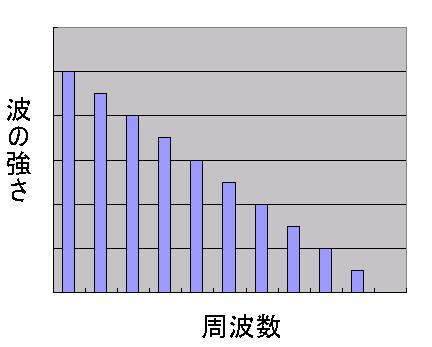
When you don not limit to three waves like above example, following chart will be the one that you will normally see. You can see that wave of longer cycle gets higher amplitude while the wave of shorter cycle gets lower amplitude.

On the other hand, the following chart indicates the result when you transform random numbers that is equally distributed and has no repetition.