更新日:2026年2月20日 Version 4.0
社会調査とデータ分析法の解説
村瀬 洋一
以下は過去の科目の記録です。2026調査実習は こちらをクリック
以前の大学院プロジェクト科目内容
計量社会学の考え方を習得し、社会調査法と多変量解析の基礎を学ぶ。各国の社会調査データを実際に分析する。大規模な社会調査に参加し調査経験を得ることも目的とする。多くの大学では社会学部であっても、本格的な統計的社会調査を経験することは少ない。積極的に参加すれば貴重な経験となる。分析ソフトは主にSPSSを使う。秋学期はAMOSを使った構造方程式モデルの実習も行う。最初はテキスト『社会調査演習 第二版』を使うので、必ず購入し、第一章を読んでおくこと。まず、無作為抽出法やコウディングや尺度構成法、調査票のワーディングなどに関する実習を行う。
文献検索法の資料
各種のデータベースについて ★検索法の解説
目次
◆AMOSについて解説資料
◆因子分析について
◆AMOS操作法の簡単な資料
村瀬WIXページ 資料PDFを少し置いている
★参考 AMOS分析の基本 YouTube動画
★参考 SPSS基本操作 YouTube動画 Rikkyo COB Data Analytics Lab
3.社会調査における社会的地位と職業分類
職業分類や職業威信スコアの見本シンタックス
職業分類作成のためのSPSSシンタックス見本
ここをクリック
クロス集計と残差の見本シンタックス
ロジスティック回帰の見本シンタックス
ロジスティック回帰の見本シンタックスその2
1995年SSM調査の階層帰属意識など
社会調査において社会的地位の変数を作る時は、以下のような主観的な社会階層か、あるいは、回答者の職業や学歴の問を元に、社会的地位の変数を作ることが多い。個人収入や世帯収入の問いを用いても良いが、無回答が多いし、収入だけでは必ずしも経済的な社会的地位をうまく測定できるわけではない。収入はフロー、資産はストックを表す。本人の収入をきいたとしても、家族の収入や、世帯全体の資産や住宅ローンの状況を把握しないと、現実の生活の豊かさは、収入をきいただけでは、必ずしもよく分からない。

4.社会構造の測定 −とくに職業分類
社会調査とその他の調査は何が違うだろうか。社会調査では、性別や年齢だけでなく、学歴や職業を正確に把握することが重要である。職業は「地位と役割」を表す総合的な指標である。例えば、ある男が40歳の銀行勤務の事務職員、ということが分かった場合、普段の生活や家族構成や収入や時間の使い方や住宅の様子などが、概ね推測可能である。つまり、社会全体では、人々の社会的地位により、収入や情報など各種の社会的資源が配分されている。その意味で、職業とは、本人の社会的地位を表す指標であり、職業を質問していない調査は、社会調査としては役に立たない。また、巨大な現代社会の中で、人々は役割分業を行っている。しかし職業と言っても、ホワイトカラーとブルーカラーに大きく2分する事も可能だし、数百の分類に分けることもできる。職業と産業は違うが、回答者の職業を定格に把握していない調査は多い。以下の「職業の4次元」をよく理解することが重要。現代日本社会には、人種による社会的亀裂や、公式な身分制度やカーストはない。しかし、医者の子が医者になり、先生の子が先生になり、各分野で二世が目立つなど、何らかの社会階層構造があることはよく知られている。これらの構造を把握するためにも、調査において職業を的確に把握することは重要である。
多くの調査では、職業の問が不十分だったり、本人の仕事内容が不明だったり、従業上の地位を質問していないので、どのような人が答えたのか良く分からない結果になっている。回答者が自営業なのか事務員なのかまるで不明というのは、大きな問題である。とくに職業分類や産業分類の理解は重要である。日本には、国勢調査の職業分類とは別に、労働省や総務省(旧行政管理庁)の職業分類がある。国際標準職業分類も存在する。日本の社会調査では、国勢調査の分類が、全国サンプルの結果と比較可能で使いやすいだろう。これをもとに簡略化したものがSSM調査職業分類であり、職業小分類は200近くある。社会調査においてよく使われる。
例えば、金融業、サービス業、自由業、教育関係、などの回答が職業だろうか。銀行勤務でも、事務員やガードマンもいれば、コンピューターの操作をする人もいる。また、的確に調査しないと、多くの人が専門職と答えるが、大卒以上の資格を持たない職は、ふつうは専門職と分類しない(専門職とは何かについては原・海野『社会調査演習 第2版』p.106参照)。機械修理の熟練工などを的確に分類することは難しい。また、管理職とは何かという定義も、調査によってまちまちでは問題である。社会調査においては、職業だけでなく、地域の都市度、産業構造、学歴などの社会的分布を正確に把握することが、きわめて重要なのである。なお産業分類は、従業先の組織の分類であり、人がやっている仕事の分類ではない。以下に、職業の4次元について解説しておく。
職業の4次元 安田三郎・原純輔.1982.『社会調査ハンドブック 第3版』p.87より
職業が社会調査において重要である理由は、職業が社会的地位と役割を表すからである。職業には貴賤がないが、職業について調査することは重要である。なぜならば、高収入の職とそうでない職が存在するし、時代によって人気がある職とそうでない職もある。また、社会的影響力の違いもあり、巨大な現代社会の中で役割分業を行っている。これらを正確に把握するためには、職業を狭義にとらえるだけでは不十分であり、以下の4次元を調査し、これらを総合する必要がある。
1)産業 −従業先の企業の分野。金融業、製造業など
2)従業先の規模 −大企業かどうかは、日本では極めて重要
3)狭義の職業(本人の仕事内容) −本人自身が何をやっているか
4)従業上の地位 −自営業か、常時雇用か、臨時雇用(パート、アルバイト、派遣社員など)
これらの他に、役職、つまり係長、課長、部長などの組織内の職位も測定することが多い。通常、日本では、課長以上を管理職とする。しかし実際に本人がやっている仕事が、管理よりも、他の仕事が多い場合は、管理職ではなく、各自の職業コードをつける。例えば、飲食店の店長といいつつ、本人が料理もやっており、仕事の大半が調理である場合は、管理職とは言えない。このため、社会調査データを処理する場合、まず管理職について、プログラム上で職業コードを修正した上で、職業分類を作ることが多い。具体的な考え方を理解するためには、原・海野『社会調査演習 第2版』2.5のコウディングの章などを、よく読むこと。『SSM調査職業分類95年版』は、501から691までの職業小分類がある。以前の日本標準職業分類には数百の職業があったが、現代日本では、炭鉱での労働者や、工場労働者などが減っており、それらを細かく分類する必要はないため、小分類の数は減っている。具体的な調査票については、SSM調査や、『社会調査演習 第2版』の巻末資料を見ること。
以下の問はaが従業上の地位、bとcが産業、dが従業先の規模、eが本人の仕事内容である。
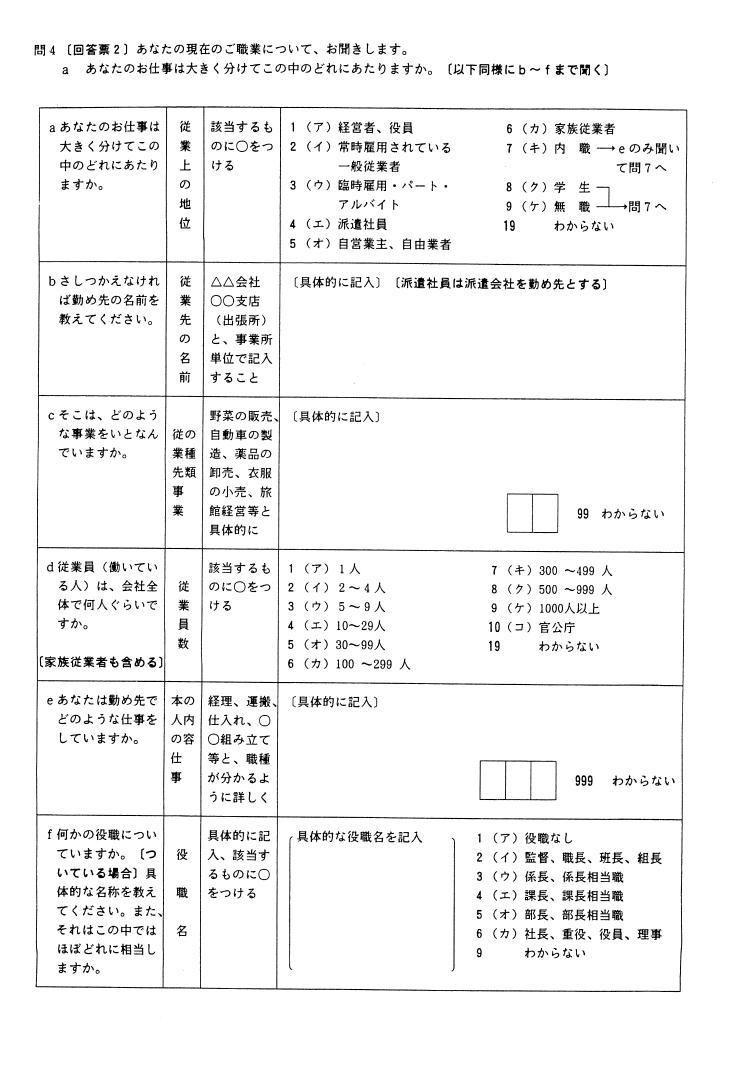
図1. 1995年SSM調査A票 本人現職
コウディングとは 原・海野『社会調査演習 第2版』p.100
社会調査において、個々の回答を記号化する(コウドをつける)という作業。社会調査では、可能な限り選択回答法(プリコウディング)で行う。しかし、職業について、100以上の選択肢から1つを選んで○をつけてもらうのは、現実的ではない。したがって、自分の職業を答えてもらい、その内容を調査後に分類してコウドをつける(501から691までの数字にする)ことになる。つまり職業については、回答の文を見てアフターコーディングする。文中に「米」や「保育」など、分かりやすい単語がある場合、コウドを間違うことはないが、現実には、分類が難しい回答もある。
社会調査において、多くのコウドは数字である。分類カテゴリーの設定は、1)カテゴリー全体が、回答の全範囲を網羅し、かつ、2)各カテゴリーは排他的でなければならない。例えば、職業(本人の仕事内容)について、501かつ524という回答はない。また、分類不能の職業(そのほとんどは回答内容不十分)は、できる限りなくすべきである。3)分類カテゴリーの区別は、合理的で明快でなくてはならない。4)分類カテゴリーの数が少なすぎると、異質の回答が混在してしまうので注意すべきである。5)他の同種の調査結果と比較できるよう、分類カテゴリーは、過去の優れた調査と類似のものを、なるべく採用すべきである。
職業の決定方法(詳しくは『社会調査演習』p.105
個人が複数の仕事をしている場合、1つの分類項目に決定する。
1)2つ以上の勤務先がある場合
ア 職業時間のもっとも長い職業。
イ アにより決めがたい場合は、収入のもっとも多い職業。
ウ 上記により決められない場合は、調査時の最近に従事した職業。
2)1つの勤務先で各種の仕事に従事しており、複数の仕事内容がある場合
ア 就業時間の長い仕事(総合判断をする)。
イ 技能が必要なもの。修理と販売なら修理にする。
現実のコウディング作業は、総合判断をどうするかが問題である。学歴や就業先規模や年齢なども見て、実際に本人がどんな仕事をしているのか、推測する必要があり、そこが難しい。
5.クロス集計の結果のまとめ方
社会調査を実施後に、データファイルが完成したら、データ分析をすることになる。もっとも基本的な分析は男女別や年代別のクロス集計である。性別の場合はカテゴリーが2つで、男女別に、2つの集計結果を出すことになる。男または女の中で、合計が100になる%を表示すればよい。縦または横%を使うこと。全体%は普通使わない。性別は2つだが、変数によっては3つ以上のカテゴリーもある。
以下のグラフは、とある社会調査における「従業上の地位」(3分類)と「情報不信」(4段階回答)のクロス集計表を横棒グラフにしたもの。

従業上の地位は、人数が多いもの3つに絞った。また分析全体を、女性で、ある年齢に絞っている。これは、性別と年齢によって働き方が異なることが予想されるからである。各カテゴリーに、1, 2, 3,と番号がついているが、これは名義尺度であり、量的意味はない。つまり、3は1の3倍の意味がある、ということではない。このような変数を質的変数という。職業や地域、都道府県(JISコード)などに番号があったとしても、量的な意味はなく、質的変数である。
質的変数間の関連係数にはいくつかのものがある。2×2表(4セル)については、原・海野(2004:85)を見ること。比率の差dとは、単なる%の差である。たとえば、ある質問項目(例えば死刑制度廃止)への賛成率が男性60%、女性50%だった場合、dは10%である。質的変数の関連係数は、2×2表(4セル)については、四分点相関係数rなどを使う。
この分析結果の背景には、どのような因果メカニズムがあるだろうか。複数を考えてみると良い。これについては、自由に解釈するしかない。豊富に解釈を出すと良いだろう。この図は、回答が3カテゴリーと4カテゴリーだから、12セルある。2×3以上の表で、質的変数の場合はクラマーのVを用いる(SPSSではなぜかクラメールのVとなっている)。
各種の関連係数について
量的変数の関連を見るためにはピアソンの積率相関計数(r)などを使うが、2×2のクロス集計表(4セル)では、基本的に四分点相関係数rを使えば良い。完全関連でなく、最大関連の時は、Q係数を使う。rの値は、完全に関連がある時は+1か−1、無関連時は0になる(原・海野.2004:85を参照)。
カイ二乗値とは、無関連時の表と、現実の表の2つを比べ、2つの距離を出したものである。各セルにその距離を書いた新たな表を作り、その値を全て二乗してから、合計するとカイ二乗値となる。試しにやってみると良い。
変数に量的な意味がある場合、2×3セル以上の表では、タウbかタウcを用いる。タウb、タウcは、無関連が0、完全関連が+1か−1となる。上記のグラフは、「情報不信」変数のカテゴリーに関しては1〜4の量的意味がある(少なくとも順序尺度ではある)と言えるが、片方が質的な場合は、表全体としては、質的変数の関連係数を使うしかない。尺度の水準については参考文献を見ること。
2×3以上の表の関連(詳しくは社会統計学の文献を見ること)
・変数に量的意味がない場合→ クラマーのV(無関連0、完全関連1)
・変数に量的意味がある場合→ タウb(3×3など対象な表) 、タウc(対象でない表) 無関連0,完全関連は+1か−1
6.エラボレイションについて
第三変数の導入による因果関係の検討をクロス集計のエラボレイション(elaboration)という。
二変数の表面的な関連は、必ずしも真の因果関係ではない。

---------------------
テキスト『社会調査演習 第2版』2.4の例は、結婚するとキャンディーを食べなくなるという例(Zeiselによる架空例)。
婚姻、食の好み、という二変数(variable)がある。二変数の間に関連があったとしても、因果関係(論理的に原因と結果になっているもの)であるとは限らない。

新たに2つ出したXとYの関連について検討する。Zを導入したことにより、XとYが無関連になれば、最初にあった関連は、疑似相関(spurious correlation)だったといってよい。
5個の関連係数を見て、真の因果関係が何かを検討することになる。詳しくはテキスト2.4「クロス集計とエラボレイション」参照。
7.系統抽出法について(『社会調査演習 第2版』2.1)
絶対誤差とは、測定値(調査結果)と、真の値(母集団における値)の差である。しかし、真の値は全数調査をしない限り分からない。
そこで、誤差を求めるために、何らかの推定をすることになる(p.55 比率の推定)。得られた結果(標本比率)は、正規分布することが知られているので、その性質をもとに、誤差の大きさを推定する。具体的には、標本比率の散らばり具合(標準偏差)をもとに、推定を行う。例えば『社会調査演習』p.53の作業をやり、全体の支持なしの値が47%、一部分を抽出した時の値(調査結果)が35%とすると、誤差(テキストにある絶対誤差イプシロン ε)は0.12となる。統計的検定における慣例では、この誤差が、ある値(標準偏差SDの1.96倍)より小さければ有意でないと判断する。つまり、ほぼt=2より小さいならば有意でない、と判断する。正確には、有意確率(危険率)αが5%の時は、有意であるかどうか判断する基準として、SDの1.96倍という値を使うことが多い。αは、誤差が有意(意味がある、ゼロではない)である可能性という意味である。αが1%の時は、誤差がある可能性は1%ある(逆にいうと、99%の確率で、誤差はない、つまり、測定値は真の値と近い)、ということになる。
★事前にSDの意味と、テキストp.165にある、両側検定の標準正規分布の図の意味を、理解しておくこと。α部分の面積が、結果が真の値からはずれている可能性である。tの値が1.959の時、αの面積が5%である。
p.32の図は、もし、たくさん調査をした時に、真の値に近い調査結果は多く、遠い調査結果は少ない、ということに関する図だと考えてよい。真ん中の値になる調査結果は、縦棒が長いので、たくさんあるという意味である。実際には、たくさん調査をすることはないが、そのように考えて、それを元に、真の値を推測することになる。図の両端は、面積が小さい。つまり、図の中心(真の値)から大きくはずれた結果が出る可能性は、少ないといってよいだろう。そのことが経験的に知られているので、その性質(正規分布の性質)をもとに、絶対誤差を推測するのである。
標本の値と、たくさんの調査結果の平均値(図の中心)との距離が、標準偏差SDと同じ(つまりt=1)だった場合
距離が1倍 t=1 31.7%
距離が2倍 t=2 4.6%
t=1.959 5.0%
距離が3倍 t=3 0.27%
つまり、標準偏差の3倍、平均値から離れている人は、0.27%しか存在しない。距離tが、絶対誤差ということになる。
ちなみに、t=2とは、日本でいう偏差値の70以上か、30以下の人のこと。
70以上の人は2.3%しか存在しない。80以上の人は0.13%しかいない。つまり、1万人が参加した試験で13人しかいないことになる。
平均値の人は偏差値50であり、たくさんいる。そのような人は、自分の値と平均値の距離がゼロである。
★『社会調査演習 第2版』p.53 作業 巻末資料の961人から、n人を選ぶ
S=3, 間隔が10ならば、3,13,23,33 … の人を選ぶ
→88人の調査対象を抽出できる。誤差が10%の時n=88くらいになるはず。
誤差が5%の時は、275人
系統抽出とは、等間隔で抽出するだけである。
n=88 ならば、
961/88 Lは約10
スタート番号Sは、Lより小さければ何でも良い。ランダムに決める。
★p.56 図2.1 2つの正規分布が重なっている。実際には、調査結果pしか分からない。
それをもとに、真の値であるPを推定する。
p は、調査結果の比率。これは、たくさん調査をすれば、たくさんありうる。
P は、母集団の値。これは1つしかないが、全員に調査をしないき限りは、分からない。しかし、全数調査は現実にはほとんどない。
例えば、調査結果の支持なしは35%、母集団においては40%だったとする。
差は5%。これが、標準偏差×1.96倍以内なのかどうか、判断する。
p.165 両側検定の危険率5%は、tの値が1.959となる。
αの面積を足すと5%。これは、調査結果が、母集団の値から大きくはずれている可能性が5%という意味。
p.32の図。たくさん調査をしたとして、端の方(母比率から大きくはずれた調査)になることは、少ない。
図の真ん中は平均値(たくさん調査をした場合)。真ん中からはずれた調査結果が出る可能性は、少ないという意味。
★標準偏差SD(standard deviation)とは、データのばらつき具合のこと。
データにはばらつきがあるから分析をするのである。全員が同じ値ならばばらつきはなく、分析の必要はない。
例えば、ある人の点数が70点、平均値が60点の場合、偏差(平均値からの距離)は10。距離とは何かを理解することがこつ。
この距離は、人によって異なる。55点の人は-5
例 10, -5, 12, -7, …
全員について、この距離を求め、距離の標準的な値を出したものが標準偏差SD。平均値60点に近い人はたくさんいる。
標準偏差の二乗が分散である。図2.1における標準偏差SDは、標準誤差と呼ばれる(p.33)。
作業と問題について
標本規模(調査人数)nが小さくなると、標本誤差εは大きくなるが、母集団人口Nが小さくても、とくに誤差には影響がない。
8.社会調査における回答者の学歴の扱い
回答者の最終学歴は、最近は高卒以下、専門学校や短大、大卒以上、の3カテゴリーに分けた新変数を作り分析することが多い。最近は、中卒以下の人数は少ないし、大学院卒も現状では比率は少ない。教育年数に直す時は、高卒は12年、大卒は16年などにして新変数を作る。社会調査の最終学歴の問において、旧制の学校制度の選択肢がある場合がある。旧制の学歴を教育年数に直す場合は、以下のSPSSシンタックスのリコード文を参考にする。1の旧制小学校は6年、2の旧制高等小学校卒は8年、7の旧制の大学は17年などにすればよい。詳しくは『社会調査演習 第二版』の巻末資料を参照。

図2. 1995年SSM調査A票 学歴
★教育年数の変数EDUを作るSPSSシンタックスの例。
1995年SSM調査A票には本人の最終学歴問10の他、父学歴、母学歴、配偶者学歴の問がある。
/***** GAKUREKI WO KYOUIKU NENSUU HE HENKAN 19960729 *****/
COMPUTE EDU=Q10S1.
COMPUTE EDUF=Q18.
COMPUTE EDUM=Q21.
COMPUTE EDUS=Q27.
RECODE EDU,EDUF,EDUM,EDUS
(1=6)(2=8)(3,4=11)(5=13)(6=14)(7=17)(12=9)(13=12)(14=14)
(15=16)(16=18)(0,19=99).
最初のページに戻る
All Rights Reserved, Copyright(c), MURASE,Yoichi













