
 |
AppendixAnalytical Method Using Equilibrium ConstantGreenwood |
1. Chemical Equilibrium Constants
Standard free energy of formation at T is defined by Gibbs-Helmholtz as
T
DG0f t= -
T∫DH0f/T2
dt
25
Integrating it, you can obtain
DG0ft = DH0f -DHt -TDS0 (kcal/kgmol)
The value of DH0f is published in Thermodynamics by Kojima 1969
DH0f (kcal/kgmol) |
|
| C |
0 |
O2 |
0 |
N2 |
0 |
CO2 |
-94,060 |
CO |
-26,416 |
H2 |
0 |
H2O |
-57,798 |
CH4 |
-17,889 |
DHt and TDS0 could also be calculated from specific heat as described in "Power Generation by Biomass Gasification Version 3"
Thus you obtain Standard free energy of formation DG0ft at T.
When you assume biomass is a pure carbon, you can define following chemical reaction and chemical equilibrium constants could be calculated for following 6 equations.
| Chemical Equations |
Name |
DH0 | Equation No. |
C + O2 = CO2 |
Oxidation |
-94,200 | 1 |
2C + O2 = 2CO |
Partial Oxidation |
-53,300 | 2 |
C + H2O = CO + H2 |
Water Gas 1 |
+31,230 | 3 |
| C + 2H2O = CO2 + 2H2 |
Water Gas 2 |
+21,560 | 4 |
| CO + 3H2 = CH4 + H2O | Methanation | -49,300 | 5 |
CO+H2O = CO2+H2 |
Shift | -9,670 | 6 |
Heat of reaction DH0 were calculated from standard heat of formation DH0f as shown below.
DH0 = (SnDH0f)prod - (SnDH0f)feed
Eq. No.1, 2, 4 and 5 having minus H0 figures are by definition, exothermic reactions. Eq. No.3 and 4 are endothermic reactions.
Finally you can calculate standard free energy of reaction at T by
DG0t = (SnDG0fti)prod - (SnDG0fti)feed
Where n is mol number of chemical equations.
Chemical equilibrium constant Kp could be calculated from standard free energy of reaction DG0t using following thermodynamic equations. Gas constant R=1.987(kcal/kgmol K)
lnKp = - DG0t/Z R T
Kp = fprod1 fprod2/ffeed
As the pressure is almost atmospheric, Z=1、fi=Pi Therefore, Kp become as follows;
Kp = Pprod1Pprod2/Pfeed
When you plot DG0 v.s.T, following diagram will be obtained.
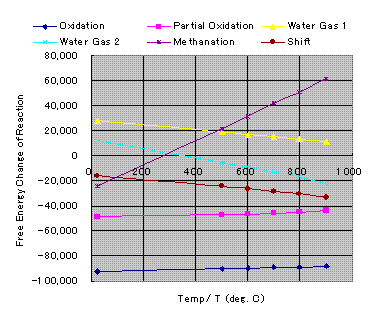
Gibbs Free Energy
Natural logarithms of chemical equilibrium constant, Kp are shown below.
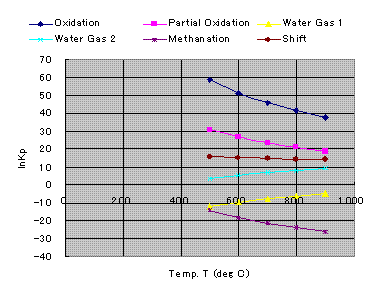
Equilibrium Constants
2. Equilibrium Calculation under Stoichiometric Constaraints (Composition Sheet)
Calculation were conducted for 400, 600, 700, 800 and 900 oC. Biomass and oxygen in Air (A) will be converted to a mixture of XO2, XCO2, XCO, XH2, XH2O, XCH4 of Gas. Number of unknown variables are 6. We have 3 equations for C, O, and H element balance as listed below.
| for C element |
C = XCO2 + XCO + XCH4 |
Eq. No. 7 |
| for O element |
2A + O = 2XO2 + 2XCO2+ XCO + XH2O |
Eq. No. 8 |
| for H element |
H = 2XH2O + 2XH2 + 4XCH4 |
Eq. No. 9 |
If we add following three equilibrium equation Kp1, Kp2, Kp3, we now have 6 algebraic equations. Here, P is total pressure and Pi is partial pressure, yi is mol fraction and SXi is a sum of all products gas mol. including nitrogen gas. Eq. No.1 to 2 are independent of total pressure.
Pi = yiP = XiP/SXi
SXi =N + XO2 + XCO2+ XCO + XH2 + XCH4 + XH2O
Here, N is nitrogen gas mol contained in the air feed.(kgmol/h)
N = XN2 = (79/21)A
| Chemical Equilibrium Constant for Eq. No.1 | Kp1 = PCO2/PO2 = (XCO2/XO2) |
Eq. No. 10 |
| Chemical Equilibrium Constant for Eq. No.2 |
Kp2 = PCO2/PO2 = (XCO2/XO2)(P/SXi) |
Eq. No. 11 |
| Chemical Equilibrium Constant for Eq. No.3 |
Kp3 = PCOPH2/PH2O = (XCOXH2/XH2O)(P/SXi) |
Eq. No. 12 |
In the early stage, from Eq. No. 7 to 12, I have obtained following equation without XO2.
(XCOXH2/XH2O)(P/KP3) + (XCO2/XCO2)(KP1/KP2)P + XCO2 + XH2O + 3XCH4-C-O-H-2A-2N = 0
But because there are still 5 unknown variables and there are so many combination of solutions. I could not find correct answer even with Solver of Excel.
Therefore, in the second stage, I have tried to reduce number of unknown variables as far as possible and reached an equation having two variables. Namely XCO2 and XCO.
From Eq. No. 7 and 9, you can eliminate XCH4 and obtain Eq. No. 13.
XH2O = 0.5H - XH2 - 2C + 2XCO2 - 2XCO Eq.No.13
From Eq. No. 8, you can obtain Eq. No. 14.
XH2O = 2A + O - 2XO2 - 2XCO2 - XCO Eq.No.14
From Eq. No. 13 and 14, you can eliminate XH2O and obtain Eq. No. 15.
0.5H - 2A - O - 2C + 2XO2 + 4XCO2 + 3XCO - XH2 = 0 Eq. No. 15
From Eq. No. 13 and 14, you can eliminate P/SXi and obtain Eq. No. 16.
KP2(XO2/XCO) = KP3(XH2O/XH2) Eq. No. 16
From Eq. No. 10, you can obtain Eq. No. 17.
XO2 = XCO2/KP1 Eq. No. 17
From Eq. No. 16 and 17, you can obtain Eq. No. 18.
(KP2/KP1)(XCO2/XCO) = KP3(XH2O/XH2) Eq. No. 18
From Eq. No. 14 and 17, you can eliminate XO2 and obtain Eq. No. 19.
XH2O = 2A + O - 2XCO2/KP1 - 2XCO2 - XCO Eq. No. 19
From Eq. No. 18, you can obtain Eq. No. 20.
XH2O = (KP2/KP1)(XCO2/XCO)(XH2/KP3) Eq. No. 20
From Eq. No. 19 and 20, you can eliminate XH2O and obtain Eq. No. 21.
(KP2KP3/KP1)(XCO2XH2/XCO) = 2A - O - 2XCO2(1/Kp1 -1) - XCO Eq. No. 21
From Eq. No. 15 and 17, you obtain
0.5H - 2A - O - 2C + 2XCO2/KP1 + 4XCO2 + 3XCO - XH2 = 0
Then you can derive Eq. No. 22.
XH2 = 0.5H - 2A - O - 2C + 2XCO2/(1/KP1+2) + 3XCO Eq. No. 22
From Eq. No.21, you obtain Eq. No. 23.
XH2 = (KP1/(KP2KP3))(XCO/XCO2)(2A - O - 2XCO2(1/Kp1 -1) - XCO) Eq. No. 23(
From Eq. No. 22 and 23, you can eliminate XH2 and obtain final objective function having two unknown variables.
0.5H - 2A - O - 2C + 2XCO2(1/Kp1+ 2)) + 3XCO - (Kp1/(Kp2Kp3))(XCO/XCO2)(2A - O - 2XCO2(1/Kp1-1) - XCO) = 0
From Eq.No.7 to 12 you can obtain following equation.
0.5H - 2A - O - 2C + 2XCO2(1/Kp1+ 2)) + 3XCO - (Kp1/(Kp2Kp3))(XCO/XCO2)(2A - O - 2XCO2(1/Kp1-1) - XCO)=0
Solver of Excel was used for numerical calculation of the above equation. Once reaction was started air is not needed. Therefore A=0. Constraints of Solver is that All Xi shall be positive figure. Minimum figure of above equation gives a set of XCO and XCO2. Then you can calculate remaining Xi as follows;
From EQ.No.7
XCH4=C-XCO2-XCO
From EQ.No.10
XO2=XCO2/Kp1
From EQ.No.8
XH2O=2A+O-2XO2-2XCO2-XCO
From EQ.No.9
XH2=0.5H-XH2O-2XCH4
January 19, 2010