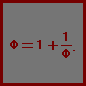| 美しい長方形 | (2)黄金比:Φ |
| 前頁の Marine の比Φ=(1+√5)/2≒1.618が、古来最も美しいとされてきた長方形の比、いわゆる黄金比です。 ピラミッド、ミロのヴィーナスやパルテノン神殿で有名であり、近年では、均整のとれた人体にこの比が現われることから、ル・コルビュジェがモジュロールの基礎にしています。音楽の世界では、バルトークが用いました。
黄金比は、正五角形の対角線にあらわれます。ユークリッドの互除法が無限に続くことが、絵を見ているだけでわかるため、恐らく人類が最初に見つけた無理(比)数ではないでしょうか。それが、この星形をシンボルとした、ピタゴラス教団の崩壊の原因ともいわれます。教団の最も重要な教義であった「万物は数(すなわち整数とその比)」を否定する無理(比)数が、あろうことかこのシンボルの中に見えているからです。 |
黄金比は、人間が意図的に用いるだけでなく、巻き貝のらせんや、植物等自然界にも現われる比としても知られています(向日葵が特に有名)。単純な規則によって生成されるフィボナッチ数列(次頁参照)と深い関係にあるため、遺伝子というプログラムに書きやすかったのでしょうか? 黄金比の長方形から、正方形をとり除いた残りの長方形は、また黄金比の長方形になります。 Φの性質●1:Φ=Φ:(1+Φ).∴Φ2=Φ+1.Φは大きい方の根を指す。小さいほうの根はΦ−1(かつΦの逆数)。●Φ=√(1+√(1+√(... ●Φ=1+1/(1+1/(...最も簡単かつ収束の遅い無限連分数 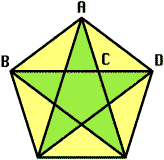 ●AB:BD=1:Φ. ●AC:AD=(Φ−1):1=1:Φ. |
|
|