平面幾何の計算 1999/02/25 (初版)
ここから定量的な計算を行います。まず、ボールの速度ベクトルを次のように大きさ
と方向(x軸となす角度)で表現することにすると、
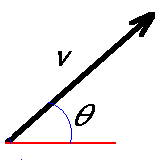
 と表現できます。これより最初のボールの位置とボールの速度(大きさと角度)を与える
とその後の1秒毎のボールの動きは決まります。
ボールの位置を1秒毎に追跡して行き、やがて壁と衝突する場合、次の図のような2つ
のタイプの衝突が考えられます。
と表現できます。これより最初のボールの位置とボールの速度(大きさと角度)を与える
とその後の1秒毎のボールの動きは決まります。
ボールの位置を1秒毎に追跡して行き、やがて壁と衝突する場合、次の図のような2つ
のタイプの衝突が考えられます。
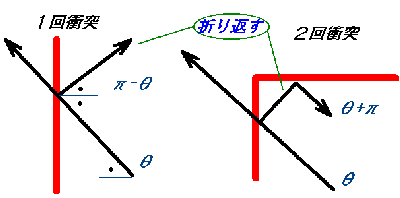 1回衝突する場合と、壁の角のところで2回衝突する場合です。その判定は図をよく見
ると分かります。1回衝突するのは、仮にボールが衝突しないで進むとしたとき、次の
ステップ(1秒後)のボールのx座標またはy座標の一方が領域を越えてはみ出す場合
です。
一方、2回衝突するのは、次のステップの座標値のx、yの両方の値がはみ出す場合
です。衝突した時刻は、速度の矢印の長さが1秒間に進む距離ですから、壁と交差する
までの長さが衝突時刻に対応します。矢印を折り返してやると、1秒後の跳ね返った位
置が決まります。
(注)ここでは、ボールの速度の大きさ(速さ)は領域に対して十分小さいとしていま
す。ボールが非常に速くて1秒間に何回も壁の端から端へ行ったり来たりするようなこ
とはないとします。
次に、ボール同士の衝突を求めます。まず、ボールが走る直線の式を求めましょう。
1回衝突する場合と、壁の角のところで2回衝突する場合です。その判定は図をよく見
ると分かります。1回衝突するのは、仮にボールが衝突しないで進むとしたとき、次の
ステップ(1秒後)のボールのx座標またはy座標の一方が領域を越えてはみ出す場合
です。
一方、2回衝突するのは、次のステップの座標値のx、yの両方の値がはみ出す場合
です。衝突した時刻は、速度の矢印の長さが1秒間に進む距離ですから、壁と交差する
までの長さが衝突時刻に対応します。矢印を折り返してやると、1秒後の跳ね返った位
置が決まります。
(注)ここでは、ボールの速度の大きさ(速さ)は領域に対して十分小さいとしていま
す。ボールが非常に速くて1秒間に何回も壁の端から端へ行ったり来たりするようなこ
とはないとします。
次に、ボール同士の衝突を求めます。まず、ボールが走る直線の式を求めましょう。
 となります。ここでいう原点とは重心のことです。この直線と原点の距離dは、衝突径数
と呼ばれるもので、その大きさが衝突を起こすかどうか、また衝突する場合にはどうのよ
うな衝突を起こすかを決めます。
となります。ここでいう原点とは重心のことです。この直線と原点の距離dは、衝突径数
と呼ばれるもので、その大きさが衝突を起こすかどうか、また衝突する場合にはどうのよ
うな衝突を起こすかを決めます。
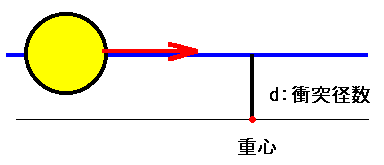 衝突でもう一つ重要な量は次の図の衝突距離です。
衝突でもう一つ重要な量は次の図の衝突距離です。
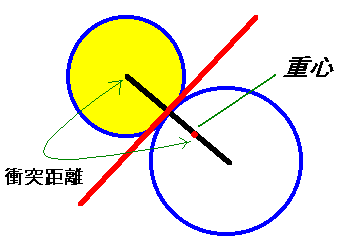 衝突距離は、2つのボールの半径と質量だけで決まります。下の図のよ
うな衝突を考えましょう。
衝突距離は、2つのボールの半径と質量だけで決まります。下の図のよ
うな衝突を考えましょう。
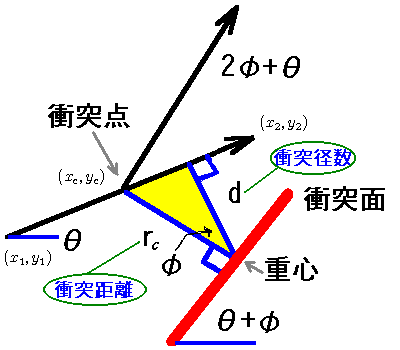 これは、ボールが角度θで重心の上側を左から右に向かって衝突する場合です。
知りたいのは衝突後の角度とボールの位置です。衝突前の直線と衝突径数は、
上記の式から求めることができるので、図の黄色い三角形の角度φが分かれば、
すべては決まります。
つまりこの図の位置関係の場合は、
これは、ボールが角度θで重心の上側を左から右に向かって衝突する場合です。
知りたいのは衝突後の角度とボールの位置です。衝突前の直線と衝突径数は、
上記の式から求めることができるので、図の黄色い三角形の角度φが分かれば、
すべては決まります。
つまりこの図の位置関係の場合は、
 衝突位置の角度が (θ+φ+π/2)になるのは、衝突面の角度が θ+φ で、この面か
らさらに90°回転したのが衝突点の位置ベクトルの方向です。
以上で、ボール同士の衝突運動を追跡することができます。次はクラスの設計です。
衝突位置の角度が (θ+φ+π/2)になるのは、衝突面の角度が θ+φ で、この面か
らさらに90°回転したのが衝突点の位置ベクトルの方向です。
以上で、ボール同士の衝突運動を追跡することができます。次はクラスの設計です。