ベクトルと行列クラスのメンバ関数の実装を完成させます。ここでは、関数同士を関 連づけながら簡単で明瞭なコーディングを行います。効率については、後で改めて考察 することにします。
3.8.1 bool型
標準C++の組み込みのデータ型には、論理型(bool型)があります。bool型は2つ
のキーワード true(真)と false(偽)のどちらかの値を持つことができる基本デ
ータ型で、論理演算の結果を表現するのに使われます。これは比較的新しく導入された
データ型で、従来のように偽を0(ゼロ)、真を非0(非ゼロ)で表すよりもプログラ
ムは読みやすくなります。
ほとんどの処理系で、bool型は1バイトで記憶されます。算術式、論理式ではbool
型はint型に変換され、trueは1に、falseは0に変わります。また、整数は暗黙の
内にbool値に変換することができます。このとき、0(ゼロ)以外の整数はtrueに、
0(ゼロ)はfalseに変換されます。
bool b; // bool型の変数
b = 5; // bはtrue
cout << b << endl; // trueではなく1が出力される
同じく、ポインタも暗黙の内にbool値に変換することができます。ポインタをbool
型の変数に代入すると、ヌルポインタはfalseに変換され、それ以外の値のポインタは
trueに変換されます。
double *ptr = new double[10000];
bool b = ptr;
if( b == false ){ // 失敗するとヌルポインタを返すnew演算子の場合
cout << "メモリ確保に失敗";
abort();
}
次に、このbool型を使った演算子の多重定義の例を示します。
3.8.2 ベクトルの等価演算子(==、!=)
等値演算子(==)と不等値演算子(!=)を多重定義して、2つのベクトルが等し いか、等しくないかを調べることができるようにします。
#include <math.h> // fabs()を使う
#define NEARLY_ZERO 1.E-16 // ゼロと見なせる
class Vector{
.........
friend bool operator==(const Vector &, const Vector &);//等しいかを判定
friend bool operator!=(const Vector &, const Vector &);// 不等号を判定
.........
}; |
これらの演算子は、左右対称な2項演算子なので非メンバ関数になり、比較のためにオ ブジェクトの要素を読み出す必要があるためにフレンド関数として定義します。
//2つのベクトルが等しいかどうかをチェックし、
//等しいときは true,等しくないときは falseを返す
bool operator==(const Vector &left, const Vector &right)
{
if(left.Dim != right.Dim)
return false; //ベクトルのサイズが異なる
for(int i = 0; i < left.Dim; i++)
if( fabs( left.ptr[i] - right.ptr[i] ) > NEARLY_ZERO )
return false; //ベクトルの内容が異なる
return true; //2つのベクトルは等しい
}
//2つのベクトルが等しくないかどうかをチェックし、
//等しいときは false,等しくないときは trueを返す
bool operator!=(const Vector &left, const Vector &right)
{
if(left == right)
return false; //2つのベクトルは等しい
else
return true; //2つのベクトルは異なる
} |
operator==()の定義で、要素の値の比較は、
for(int i = 0; i < left.Dim; i++)
if( left.ptr[i] != right.ptr[i] ) // 等しくない
return false;
とすることもできますが、計算誤差の範囲内で等値性を判定する方が確実です。
if( fabs( left.ptr[i] - right.ptr[i] ) > NEARLY_ZERO )
ここで、NEARLY_ZERO はゼロと見なせる範囲の値でヘッダファイルでマクロ定義して
あります。
3.8.3 その他のメンバ関数
ベクトルのマイナスすなわち、 −x; も扱えるようにします。これはベクトルの符号反転を返します。ただし、オブジェクト そのものは変化しません。この場合は、メンバ関数として実装する方が簡単です。
class Vector{
.........
public:
..........
const Vector operator-() const { return -1.0*(*this);} // (-1)ベクトル
.........
double norm() const; // ノルムを求める
const Vector &normalize(); // ベクトルの規格化
.......
}; |
このメンバ関数(従ってthisポインタが使える)は、ベクトルの実数倍 operator*(-1.0, *this) を呼び出します。 次に、ベクトルの大きさ(ノルム)を求めるメンバ関数 double Vector::norm() const; // ノルムを求める と単位ベクトルに変換(規格化)するメンバ関数 const Vector &Vector::normalize(); // ベクトルの規格化 を定義します。
// ノルムの計算
double Vector::norm() const
{
double a = 0.0;
for(int i = 0; i < Dim; i++)
a += ptr[i]*ptr[i];
return sqrt( a );
}
// ベクトルを規格化(オブジェクト自身が規格化される)
const Vector &Vector::normalize()
{
double a = norm();
if(a < NEARLY_ZERO) return *this; // ノルムゼロのベクトル
for(int i = 0; i < Dim; i++)
ptr[i] /= a;
return *this;
} |
次に、行列の演算(和、差、積)及びベクトルと行列の演算(積)について、多重定 義します。行列同士の足し算と引き算はベクトルの時と同じように定義できます。つま り、足し算+は演算子+=と関連付けて多重定義します。引き算−は、演算子−=と関 連付けます。 しかし、掛け算*についてはもう少し微妙で複雑です。まずは、インターフェースを 示します。
class Matrix; // 前方宣言
// 非メンバ関数
const Matrix operator+(const Matrix &, const Matrix &);// 行列の和
const Matrix operator-(const Matrix &, const Matrix &);// 行列の差
class Matrix{
......
friend const Matrix operator*(const Matrix &, const Matrix &);// 積
friend const Vector operator*(const Matrix &, const Vector &);
friend const Vector operator*(const Vector &, const Matrix &);
friend bool operator==(const Matrix &, const Matrix &);// ==演算子
friend bool operator!=(const Matrix &, const Matrix &);// !=演算子
.....
public:
.....
Matrix &operator+=(const Matrix &); // +=演算子
Matrix &operator-=(const Matrix &); // -=演算子
Matrix &operator*=(const Matrix &); // *=演算子
......
}; |
// 多重定義された +=演算子
Matrix &Matrix::operator+=(const Matrix &right)
{
if((Row != right.Row) || (Col != right.Col)){//サイズのチェック
cout << "エラー:行列のサイズが一致しません\n";
abort();
}
for (int i = 0; i < Row; i++)
ptr[i] += right.ptr[i]; // ベクトルの演算子+=を使う
return *this;
}
// 多重定義された -=演算子
Matrix &Matrix::operator-=(const Matrix &right)
{
if((Row != right.Row) || (Col != right.Col)){//サイズのチェック
cout << "エラー:行列のサイズが一致しません\n";
abort();
}
for (int i = 0; i < Row; i++)
ptr[i] -= right.ptr[i]; // ベクトルの演算子−=を使う
return *this;
} |
ここで、ベクトルの演算子+=や演算子−=を使っていることに注目しましょう。 足し算と引き算は、これらの演算子を使うと簡単に定義することができます。
// 多重定義された+演算子
// 2つの行列の和を求め、値渡しで返す
const Matrix operator+(const Matrix &left, const Matrix &right)
{
Matrix m = left; //一時的なオブジェクトを作る
return m += right; // 演算子 += を使う
}
// 多重定義された−演算子
// 2つの行列の差を求め、値渡しで返す
const Matrix operator-(const Matrix &left, const Matrix &right)
{
Matrix m = left; //一時的なオブジェクトを作る
return m -= right; // 演算子 -= を使う
} |
演算子+と演算子−が、const Matrixを返す理由は §3.7.4 をご覧ください。 一方、掛け算についてはこの様な方法は使えません。コードを書く前に、掛け算の規 則をまとめておきます。
3.8.5 ベクトルと行列の演算規則
本来ベクトルと行列の演算では、ベクトルを横ベクトルと縦ベクトルで表現します。
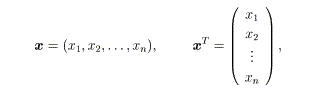
つまり、横ベクトルを1行n列の行列と見なし、縦ベクトルをn行1列の行列と見なす ことにより、ベクトルを行列の仲間として扱います。縦ベクトル記号の添え字Tは転置 (transposed)を表し、行と列の交換を意味します。この様な表現法を使うと、ベクト ルの内積は次のように表せます。
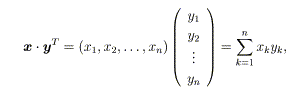
すなわち、ベクトルの内積とは同じ次元数の横ベクトルと縦ベクトルの演算であり、左 側が横ベクトルで、右側が縦ベクトルです(演算はすべて「ヨコ×タテ」です)。 一方、プログラミングではベクトルをこの様に横と縦に区別して表現しません。また 行列の内部表現の性質から、横ベクトル(行ベクトル)を扱う方を得意とします。次に演算を考えます。m行n列の行列
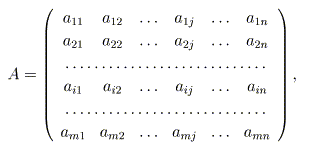
に対して、n次元のベクトルxを右側から掛けるとm次元のベクトルができます。 これ は、
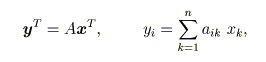
という式で表されて、次のような構造をしています。
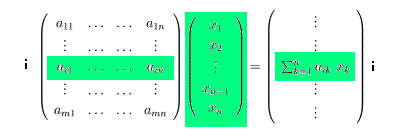
行列とベクトルの積は、行ベクトル(横ベクトル)要素とベクトルの内積を要素に持つ ベクトルです。 また、m次元ベクトルxにm行n列の行列Aを右側から掛けると、n次元ベクトルが できます。
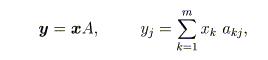
この掛け算は、横ベクトルと行列の列ベクトル(縦ベクトル)要素との内積を意味しま す。つまり、
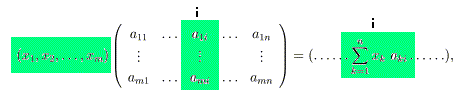
という構造をしています。
以上の規則から、行列同士の掛け算が導かれます。(L×M)の行列Aに(M×N) の行列Bを掛けると、(L×N)の行列ができます。
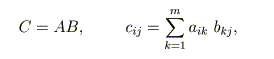
これは、次のような構造をしています。
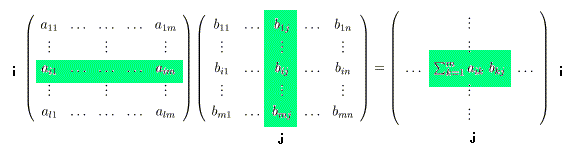
行列の積は、行ベクトルと列ベクトルの内積です。掛け算のi行j列要素は、左側行列 の「i行ベクトル」と右側行列の「j列ベクトル」との内積です。
3.8.6 ベクトルと行列の演算子(*)の実装
ベクトルと行列の掛け算、「行列×ベクトル」及び「ベクトル×行列」の演算を実装 します。プログラムでは、横ベクトルの扱いを得意とすることを考慮すると、行列を次 のように行ベクトルの並びとして表現しておきます。
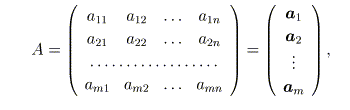
ここで、行列オブジェクトAの第(i+1)行ベクトル(横ベクトル)は A.ptr[i]; // (i+1)番目の行ベクトル です。すると、「行列×ベクトル」は次のように書けます。
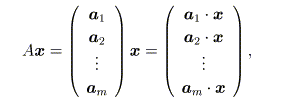
ただし、転置記号Tは省略しています。これは、掛け算がベクトルの内積で書き表せる ことを示しています。 A.ptr[i] * x; // (i+1)番目要素(行ベクトル)とベクトルの内積 一方「ベクトル×行列」の方は、要素同士の掛け算を明示的にコーディングしなけれ ばなりません。
// 多重定義された*演算子
// 行列とベクトルの積を求め、値渡しで返す
const Vector operator*(const Matrix &a, const Vector &x)
{
if(a.Col != x.getSize()){//サイズのチェック
cout << "エラー:行列とベクトルの型が一致しません\n";
abort();
}
Vector y( a.Row ); //一時的なオブジェクトを作る
for(int i = 0; i < a.Row; i++)
y[i] = a.ptr[i] * x; // 行ベクトル*ベクトル(内積)
return y;
}
// 多重定義された*演算子
// ベクトルと行列の積を求め、値渡しで返す
const Vector operator*(const Vector &x, const Matrix &a)
{
if(a.Row != x.getSize()){//サイズのチェック
cout << "エラー:ベクトルと行列の型が一致しません\n";
abort();
}
Vector y( a.Col ); //一時的なオブジェクトを作る
for(int i = 0; i < a.Col; i++){
double sum = 0.0;
for(int j = 0; j < a.Row; j++)
sum += x[j] * a.ptr[j][i];
y[i] = sum;
}
return y;
} |
次は、行列同士の掛け算の実装です。これは、「ベクトル×行列」の演算を利用しま す。
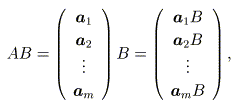
と書き表すことができますので、次のような実装になります。
// 多重定義された*演算子
// 2つの行列の積を求め、値渡しで返す
const Matrix operator*(const Matrix &left, const Matrix &right)
{
if(left.Col != right.Row){//サイズのチェック
cout << "エラー:行列の型が一致しません\n";
abort();
}
Matrix m(left.Row, right.Col); //一時的なオブジェクトを作る
for (int i = 0; i < left.Row; i++)
m.ptr[i] = left.ptr[i] * right; // 行ベクトル*行列
return m;
}
// 多重定義された*=演算子
Matrix &Matrix::operator*=(const Matrix &right)
{
if((Col != right.Row) || ((Col != right.Col))){//サイズのチェック
cout << "エラー:行列の型が一致しません\n";
abort();
}
return *this = (*this) * right; // 行列*行列を使う
} |
演算子+の場合と違って、演算子*は*=を使って書けないことに注意しましょう。 行列オブジェクトA、Bについて A *= B; // A = A * B; は、行列Bが正方行列(square matrix)でなければなりません。そうでないと、掛け 算「A*B」は行列Aとは違うサイズの行列になります。 つまり、演算子*=の方が、演算子*よりも適用される行列の条件がきつくなってい ます。
3.8.7 行列の等価演算子(==、!=)
最後に、行列に対する等値演算子(==)と不等値演算子(!=)を多重定義します。
//2つの行列が等しいかどうかをチェックし、
//等しいときはtrue,等しくないときは falseを返す
bool operator==(const Matrix &left, const Matrix &right)
{
if(left.Row != right.Row || left.Col != right.Col) //サイズが違う
return false;
for(int i = 0; i < left.Row; i++)
if( left.ptr[i] != right.ptr[i])
return false; // 行列の内容が違う
return true; // 2つの行列は等しい
}
//2つの行列が等しくないかどうかをチェックし、
//等しいときは0,等しくないときは1を返す
bool operator!=(const Matrix &left, const Matrix &right)
{
if(left == right)
return false; //2つの行列は等しい
else
return true; //2つの行列は異なる
} |
行列要素の比較に、ベクトルに関する不等値演算子(!=)を使っています。
for(int i = 0; i < left.Row; i++)
if( left.ptr[i] != right.ptr[i]) // 行ベクトルの不等値をテスト
return false; // 行列の内容が違う
また2番目の演算子関数定義は、1番目の演算子関数operator==()を使っています。
次のページでは、ここで設計したメンバ関数(及び非メンバ関数)の機能確認のため
の例題をいくつか取り上げます。
| 目次 | 前のページ | 次のページ | ページの先頭 |
Copyright(c) 1999 Yamada, K