２変数関数の３次元プロット描画等では、透視図法を次のように扱います。 

　３次元空間の物体を見る視点座標を導入し、その視点から見
た透視図形を描く。 
　透視の効果は物体と視点との距離で決まるので、視点座標を
極座標（ρ,θ,φ）で与える。 
　このとき、視点が見る物体の中心である注視点を中心とする
平面を透視平面として描く。 
　透視図法の他に、直交射影図法も扱えるようにする。 
これは、視点が無限遠点の場合の透視図です。直交射影では、
平行線は平行のまま描かれます。 



１．視点座標の設定

　視点座標（下図のＥ）は、極座標（ρ,θ,φ）で与えます。 
ここで、 

     ρ (rho)  :視点の原点からの距離 
     θ (theta):視点のｘ軸からの水平方向の角度（０〜３６０度） 
     φ (phi)  :視点のｚ軸からの垂直方向の角度（０〜１８０度） 


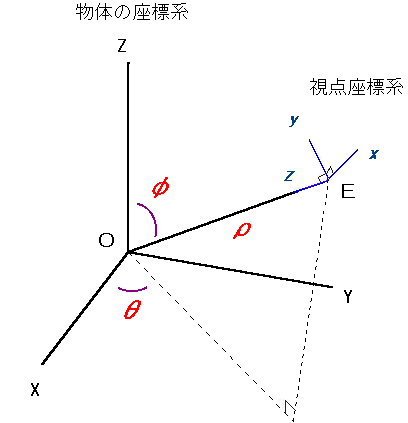とρ,θ,φは定義されます。つまり、ρは注視点Ｏ（物体の中心）と視点Ｅ
との距離で、透視の効果を現すパラメータとなります。この値が小さいほど
効果は強くなります。また（θ,φ）は視点の方向を現します。 
　描かれる図形は、注視点Ｏを含む、直線ＥＯに垂直な平面に射影されます。
このとき注視点は、透視平面の中心になります。
　注視点は設定を省略すると、デフォルト値である原点になります。

　また、パラメータρを負の値にしたとき、直交射影（視点が無限遠）と 
いう規約とします。 

　プログラムでは、視点はメンバー関数GRAPH::eye()で、注視点はメンバー
関数GRAPH::center() で設定します。
　設定後は、透視平面の座標値はGRAPH::perspective() （透視座標変換）を
使って得ることができます。透視図形は、この透視座標変換の値を使って描き
ます。


       透視座標の数学表現はこちら


２．サンプルによる例


　いろいろな角度から見た立方体
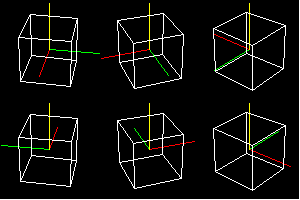ソース・ファイル（eye02.cpp）


　2変数の数学関数のプロット
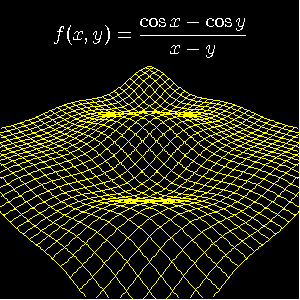ソース・ファイル（eye04.cpp）


トーラス
ソースファイル(eye07.cpp)

| 戻る |
 

Copyright(c) 1998-2002 Yamada, K