|
数学ハンドブック | 公式集 （面積・体積・・） | 公式集−断面性能 | 記号−単位 | |
|
物理学ハンドブック | 公式集−乗法公式・因数分解 | . | . | . |
ヘロンの公式 |
 |
sin2θ ＋ cos2θ = １ --- （１）
公式（１）を変形して、因数分解すると
sin2 A ＋ cos2 A = １
sin2 A ＝ １ − cos2 A ＝ （ １＋ cos A ） （ １− cos A ） --- ( 2 )
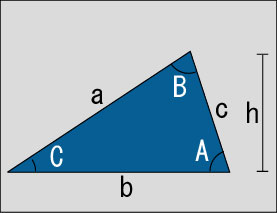
余弦定理より
a2 = b2 + c2 - 2bc cos A --- ( 3 )
公式（ 3 ）より、
cos A = ( b2 + c2 - a2 ) ／ ( 2bc )
これを、すこし細工して、
１ ＋ cos A ＝ ( 2bc + b2 + c2 - a2 ) ／ ( 2bc ) ＝ ｛ ( b + c )2 - a2 ｝ ／ ( 2bc )
＝ ｛ ( b + c + a ) ( b + c - a ) ｝ ／ ( 2bc )
ここで、 a + b + c = 2s とおけば、
b + c - a = 2s - 2a = 2( s - a )
∴ １ ＋ cos A ＝ ｛ ( b + c + a ) ( b + c - a ) ｝ ／ ( 2bc ) ＝ ｛ 2s 2( s - a ) ｝ ／ ( 2bc )
∴ １ ＋ cos A ＝ 2s ( s - a ) ／ ( bc ) --- ( 4 )
同様に
１ − cos A ＝ ( 2bc - b2 - c2 + a2 ) ／ ( 2bc ) ＝ ｛ a2 - ( b - c )2 ｝ ／ ( 2bc )
＝ ｛ ( a + b - c ) ( a - b + c ) ｝ ／ ( 2bc )
ここで、 a + b + c = 2s とおけば
a + b - c = 2s - 2c = 2( s - c )
a - b + c = 2s - 2b = 2( s - b )
∴ １ − cos A ＝ ｛ ( a + b - c ) ( a - b + c ) ｝ ／ ( 2bc ) ＝｛ 2( s - c ) 2( s - b ) ｝ ／ ( 2bc )
∴ １ − cos A ＝ 2( s - b ) ( s - c ) ／ ( bc ) --- ( 5 )
式（４） （５）を 式 （２）に代入すると
sin2 A ＝ （ １＋ cos A ） （ １− cos A ）
＝ 2s ( s - a ) ／ ( bc ) × 2( s - b ) ( s - c ) ／ ( bc )
＝ 4 s ( s - a ) ( s - b ) ( s - c ) ／ ( b2 c2 )
∴ sin A ＝ √ ｛ s ( s - a ) ( s - b ) ( s - c ) ｝ × 2 ／ ( bc )
三角形の面積は、 面積 ＝ bh／2
h ＝ c sin A より、
面積＝bh／2 ＝ ( bc sin A ） ／ 2 ＝ √ ｛ s ( s - a ) ( s - b ) ( s - c ) ｝
となります。
丶 jin 丶