| 美しい長方形 | (3)フィボナッチ数:Fn |
| 直前の2つの数字を加えたものが次の数字となる数列を、フィボナッチ数列と呼びます。 1,1,2,3,5,8,13,21,34,55,89,144,233,377,... フィボナッチ(Fibonacci=Leonardo da Pisa, 1174?-1250?, Liber abaci(1202)を著す。)が、「つがいの兎が、毎月1組のつがいの兎を生むものとすると、一年後には何組のつがいの兎がいることになるか?」という問題を考えたからです。わかり易いように最初を1,1,で始めることになっています。 F5=5,F10=Σ10=55,F12=122=144等は覚えやすいです。F12,F13,F14が、それぞれ144,233,377となるのも覚えやすいです。377/233は黄金比の大変よい近似値です。 この数列は自然界においてよく現われる数列です。例えば、幹の回りに螺旋状に生える植物の葉の、となりあう2つの葉のなす角は、フィボナッチ数列からひとつおきに数字をとったものの比になることが知られています。この比は、Φ-2=1/(1+Φ)≒0.382、約137.5°(すなわち円周を黄金分割する角度)に収束します。 |
フィボナッチ数列の性質●Fn+2=Fn+1+Fn●Fn={(1+√5)n-(1−√5)}/2n√5 ●Fn+1/Fn→Φ(n→∞)フィボナッチ数列の隣り合う2項の比は黄金比に収束します。 ●Fn-1Fn+1−Fn2=(-1)n.サムロイドの長方形分割パズルは、この性質に基づいて作られています。 ●FnFn+1=ΣFi2(i=1..n).これは、黄金比の長方形の中に正方形を書いた次の図からもわかります。 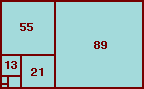 正方形の並べ方を変えると、(巻き貝の)螺旋形が現われます。極限的にBernoulli螺旋=対数螺旋=等角螺旋となり、自分自身と相似です。  |