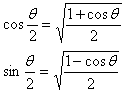 特に、cosθ=a/2 の時、分母をルートの外に出すと、
特に、cosθ=a/2 の時、分母をルートの外に出すと、
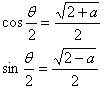 これにより、n=4, 8, 16, 32, 64 の場合の解が得られる。
結果だけ書くと、
n=4
これにより、n=4, 8, 16, 32, 64 の場合の解が得られる。
結果だけ書くと、
n=4
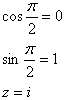 n=8
n=8
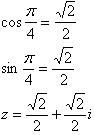 n=16
n=16
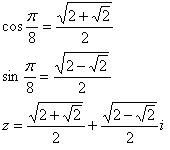 n=32
n=32
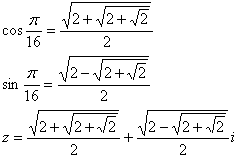 n=64
n=64
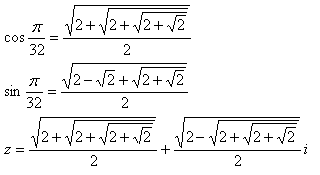
z^n-1=0 は、円周等分多項式であり、解は、
z=x+yi
=cos(2pi.k/n)+sin(2pi.k/n)i (k=0,1,...,n-1)
で表される。
実部 Re(z)=cos(2pi.k/n)
虚部 Im(z)=sin(2pi.k/n)
である。
|z|=sqrt(cos(2pi.k/n)^2+sin(2pi.k/n)^2)
=1
なので、実部 x=cos(2pi.k/n) が分かれば、虚部は、sqrt(1-x^2) で求められる。
任意の n について、
z^n-1=(z-1)(z^(n-1)+z^(n-2)+...+z+1)
なので、z^n-1=0 は、自明な解 z=1 を持つ。
よって、2≦n≦100 の素数について、自明でない最初の解、
z_1=cos(2pi/n)+sin(2pi/n)
の、ベキ根と四則演算による表現を求める。
残りの解は、三角関数の倍角定理と加法定理で計算できるので、ここでは省略。
最初は n=2 の場合。z= -1 となる。 (以下、z_1 と書かず、単に z と表す) 次は n=3 だが、後回しにして、n=4 以降の 2のベキ乗の場合を、三角関数の半角公式で一気に求める。 半角公式特に、cosθ=a/2 の時、分母をルートの外に出すと、
これにより、n=4, 8, 16, 32, 64 の場合の解が得られる。 結果だけ書くと、 n=4
n=8
n=16
n=32
n=64
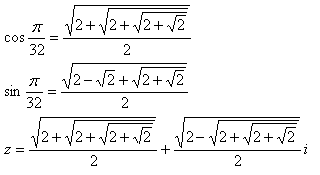
次は n=3 の場合。これは2次方程式となり、解は、この解に半角公式を適用することにより、n=6, 12, 24, 48, 96 の場合の解が得られる。 結果だけ書くと、 n=6
n=12
n=24
n=48
n=96
(注:このように、2 のベキ乗、3×2のベキ乗の場合は、漸化的に計算できるので、 微積分以前(円周率の公式が発見される以前)は、円周率計算でよく用いられた。)
次は n=5 の場合。z^4+z^3+z^2+z+1=0 となり見掛けは4次式だが、 t=z+1/z と置き換えることにより、2次方程式を2回解くことによって解が得られる。 解は、当然、 cos(2pi/5)=(sqrt(5)-1)/4 sin(2pi/5)=(sqrt(10+2sqrt(5)))/4 後に5次方程式を解くとき、z1 に対する z12=z2 z13=z3 z14=z4 の値を必要とするので、全部求めておくと、
この解に半角公式を適用することにより、n=10, 20, 40, 80 の場合の解が得られる。 特に、cosθ=a/4 の時、分母をルートの外に出すと、 cos(θ/2)=(sqrt(8+2a))/4 sin(θ/2)=(sqrt(8-2a))/4 結果だけ書くと、 n=10
n=20
n=40
n=80
ここで使った t=z+1/z という置き換えはひじょうに強力で、 これ以降、解を求める場合の基本的なテクニックとなる。 |z|=1 より、
なので、 t=z+1/z =2Re(z) となり、実数となる。実数であることがわかるので、その後の計算が見通しのよいものとなる。 この後、解を求めるに当たって、 z_k=cos(2pi.k/n)+sin(2pi.k/n).i と z_(n-k)=cos(2pi.(n-k)/n)+sin(2pi.(n-k)/n).i をペアにして、 t_k=z_k+z_(n-k) という置き換えを駆使するが、 cos(2pi.(n-k)/n)= cos(2pi.k/n) sin(2pi.(n-k)/n)= -sin(2pi.k/n) なので、 t_k=2Re(z_k) =2cos(2pi.k/n) となる。これは必ず実数であり、図形的考察により正負、大小関係が簡単にわかるので、 方程式を解いた時、どの値を t_k として選択するかを判断するのに役立つ。
次に最小となるのは n=7 の場合。 z^6+z^5+z^4+z^3+z^2+z+1=0 に対して、t=z+1/z の置き換えで、 t^3+t^2-2t-1=0 となり、y=t+1/3 の置き換えで、 y^3-7/3y-7/27=0 となる。カルダノの公式を適用してこの3次方程式を解き、変数を元に戻すと、 z=cos(2pi/7)+sin(2pi/7).i根号の中の分数を外に出すと、
a=1+3sqrt(3)i, a~ を a の共役とすると、 12.Re z = cbrt(28a) + cbrt(28a~) - 2, 12.Im z = sqrt{ 84 + 4cbrt(28a) + 4cbrt(28a~) - 2cbrt(49a^2) - 2cbrt(49(a~)^2) } (このぐらいになると、数式エディタを使って、分数・ベキ乗根が明示的にわかるようにしないと苦しい。 例えば、"TeXclip 2.0" http://maru.bonyari.jp/texclip/ は、 Web上で TeX式を入力し、画像イメージで生成することができる。) n=7 に半角公式、1/3角公式を適用することにより、 n=14, 28, 56 n=21, 42, 84 n=63 の場合が得られる。 以下、3次方程式を何回も解くことになるが、一般に2乗の項の係数が0でないことが多いので、
に対する解の公式を書き下しておく。 y=x+a/3 とおくと、
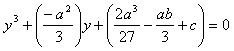
とおくと、 u^3=-q/2+sqrt(r) v^3=-q/2-sqrt(r) y=cbrt(u^3)+cbrt(v^3)
∴ x=y-a/3
sqrt(r)の分母を外に出すと、 a^3c/27-a^2b^2/108-abc/6+b^3/27+c^2/4
q/2=a^3/27-ab/6+c/2
u^3=(-2a^3+9ab-27c)/54+sqrt(12a^3c-3a^2b^2-54abc+12b^3+81c^2)/18
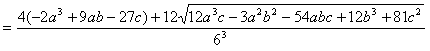
或いは、
とおき、
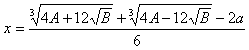
2次方程式だけで解けるもう一つの値 n=17 の場合を求める。
z^16+z^15+...+z+1=0
に対し、
z_k=cos(2pi.k/17)+sin(2pi.k/17).i
と
z_(17-k)=cos(2pi.(17-k)/17)+sin(2pi.(17-k)/17).i
のペアリングにより、2次方程式に帰着させることができる。
17の原始根(例えば 3) を使って、z を順に 3乗 (mod 17) したもの、
z, z^3, z^9, z^27=z^10, z^30=z^13, z^39=z^5, z^15, z^45=z^11, z^33=z^16,
z^48=z^14, z^42=z^8, z^24=z^7, z^21=z^4, z^12, z^36=z^2, z^6, z^18=z
を2つに分ける(1つおきに組み合せる)
p0=z+z^9+z^13+z^15+z^16+z^8+z^4+z^2
p1=z^3+z^10+z^5+z^11+z^14+z^7+z^12+z^6
ベキだけ書くと、
p0={1,9,13,15,16,8,4,2}
p1={3,10,5,11,14,7,12,6}
p0+p1= -1
p0p1=(計算すると)= -4
よって、p0, p1 は、2次方程式 p^2+p-4=0 の解。
図形的考察により、p1<p0 がわかる。
p0=(-1+sqrt(17))/2
p1=(-1-sqrt(17))/2
a=sqrt(17)
とおくと、
p0=(-1+a)/2
p1=(-1-a)/2
次に p0, p1 をそれぞれ2つに分ける(1つおきに組み合せる)
q0={1,13,16,4}
q1={3,5,14,12}
q2={9,15,8,2}
q3={10,11,7,6}
q0+q2=p0, q0q2= -1
q1+q3=p1, q1q3= -1
より、
q0,q2 は、2次方程式 q^2-p0q-1=0 の解
q1,q3 は、2次方程式 q^2-p1q-1=0 の解
図形的考察により、q2<q0, q3<q1 がわかる。結果だけ書くと、
q0=(-1+a+sqrt(2(17-a)))/4
q2=(-1+a-sqrt(2(17-a)))/4
q1=(-1-a+sqrt(2(17+a)))/4
q3=(-1-a-sqrt(2(17+a)))/4
次に q0, ..., q3 を2つに分ける(1つおきに組み合せる)
r0={1,16}, r4={13,4}
r1={3,14}, r5={5,12}
r2={9,8}, r6={15,2}
r3={10,7}, r7={11,6}
r0+r4=q0, r0r4={3,5,12,14}=q1
r1+r5=q1, r1r5={2,8,9,15}=q2
r2+r6=q2, r2r6={6,7,10,11}=q3
r3+r7=q3, r3r7={1,4,13,16}=q0
より、
r0, r4 は、2次方程式 r^2-q0r+q1=0 の解
r1, r5 は、2次方程式 r^2-q1r+q2=0 の解
r2, r6 は、2次方程式 r^2-q2r+q3=0 の解
r3, r7 は、2次方程式 r^2-q3r+q0=0 の解
r4<r0
r=(q0+/-sqrt(q0^2-4*q1))/2
z+z16=z+1/z=(2Re(z)=2cos(2pi/17))=r0
より、cos(2pi/17)が求められる。
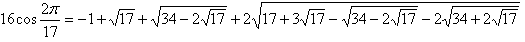 sinの方も含めると、
sinの方も含めると、
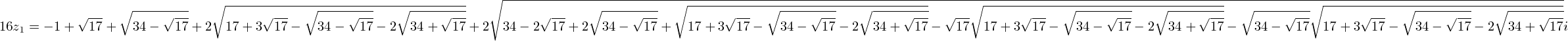 注:上記の計算で、どちらの根を選択するかは、図形的考察によりほぼ明らか。
よくわからない時は、cos(2pi.k/17) の値を直接計算して比較すればよい。
n=17 に半角公式、1/3角公式を適用することにより、
n=34, 68
n=51
の場合が得られる。
注:上記の計算で、どちらの根を選択するかは、図形的考察によりほぼ明らか。
よくわからない時は、cos(2pi.k/17) の値を直接計算して比較すればよい。
n=17 に半角公式、1/3角公式を適用することにより、
n=34, 68
n=51
の場合が得られる。
n=13 の場合、
z^12+z^11+...+z+1=0
これも、n=17 の時と同じように、13の原始根(例えば 2)を元に、z から始めて次々に2乗し、
z, z^2, z^4, z^8, z^16=z^3, z^6,
z^12, z^24=z^11, z^22=z^9, z^18=z^5, z^10, z^20=z^7, (z^14=z)
適当にペアリングすることにより、2次方程式、3次方程式に帰着できる。
n-1 が 2 と 3 のベキ乗のみで表される素数、
n=19, 37, 73, 97 の場合も、同じ要領で解くことができる。
----[n=13 の場合の概略:ここから]----
1個おきに足す
y1=z+z^4+z^3+z^12+z^9+z^10
y2=z^2+z^8+z^6+z^11+z^5+z^7
ベキだけ書き出すと、
y1={1,4,3,12,9,10}
y2={2,8,6,11,5,7}
y1+y2= -1, y1y2=(計算すると)= -3
よって、y1, y2 は、
y^2+y-3=0
の解。
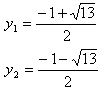 次に、y1 を3分割(2個おきに足す)
f1={1,12}
f2={4,9}
f3={3,10}
f1+f2+f3=y1, f2f3+f3f1+f1f2=(計算すると)=-1, f1f2f3=(計算すると)=y2+2
よって、f1, f2, f3 は、
次に、y1 を3分割(2個おきに足す)
f1={1,12}
f2={4,9}
f3={3,10}
f1+f2+f3=y1, f2f3+f3f1+f1f2=(計算すると)=-1, f1f2f3=(計算すると)=y2+2
よって、f1, f2, f3 は、
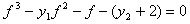 の解。
f=g+y1/3
とおくと、
の解。
f=g+y1/3
とおくと、
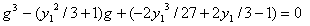
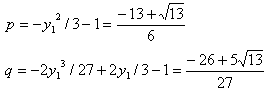 とおくと、
(q/2)^2+(p/3)^3= -13/108 = -39/18^2
u^3,v^3= -(q/2) +/- sqrt((q/2)^2+(p/3)^3)
u,v = cbrt((26-5sqrt(13))/54 +/- sqrt(39)i/18)
とおくと、
(q/2)^2+(p/3)^3= -13/108 = -39/18^2
u^3,v^3= -(q/2) +/- sqrt((q/2)^2+(p/3)^3)
u,v = cbrt((26-5sqrt(13))/54 +/- sqrt(39)i/18)
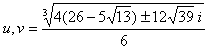 g1=cbrt(u^3)+cbrt(v^3)
g1=cbrt(u^3)+cbrt(v^3)
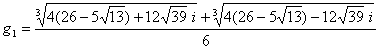 これらは3つとも実根で、g3<g2<g1 より、それぞれの値を決定。
f1=g1+y1/3
これらは3つとも実根で、g3<g2<g1 より、それぞれの値を決定。
f1=g1+y1/3
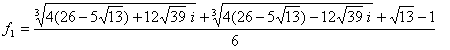 f1=z+z^12=2cos(2pi/13)
より、
f1=z+z^12=2cos(2pi/13)
より、
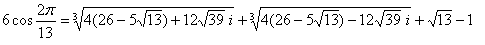 ----[n=13 の場合の概略:ここまで]----
----[n=19 の場合の概略:ここから]----
z から始めて、2乗していく
z, z^2, z^4, z^8, z^16, z^32=z^13, z^26=z^7, z^14, z^28=z^9, z^18,
z^36=z^17, z^34=z^15, z^30=z^11, z^22=z^3, z^6, z^12, z^24=z^5, z^10, z^20=z
2個おきに足す(ベキだけ表す)
y1={1,8,7,18,11,12}
y2={2,16,14,17,3,5}
y3={4,13,9,15,6,10}
y1+y2+y3=-1
y2y3+y3y1+y1y2=(計算すると)=-6
y1y2y3=(計算すると)=7
よって、y1, y2, y3 は、
----[n=13 の場合の概略:ここまで]----
----[n=19 の場合の概略:ここから]----
z から始めて、2乗していく
z, z^2, z^4, z^8, z^16, z^32=z^13, z^26=z^7, z^14, z^28=z^9, z^18,
z^36=z^17, z^34=z^15, z^30=z^11, z^22=z^3, z^6, z^12, z^24=z^5, z^10, z^20=z
2個おきに足す(ベキだけ表す)
y1={1,8,7,18,11,12}
y2={2,16,14,17,3,5}
y3={4,13,9,15,6,10}
y1+y2+y3=-1
y2y3+y3y1+y1y2=(計算すると)=-6
y1y2y3=(計算すると)=7
よって、y1, y2, y3 は、
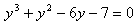 の解
y1, y2, y3 は全て実数で、大小関係は、図形的考察により、
y2が一番大きい。y1とy3は計算してみないと不明。
y1=z+z^8+z^7+z^18+z^11+z^12 = -1.2218761622631909348
y2=z^2+z^16+z^14+z^17+z^3+z^5 = 2.5070186440929762999
y3=z^4+z^13+z^9+z^15+z^6+z^10 = -2.2851424818297853656
∴ y3<y1<0<y2
y=g-1/3 とおくと、
の解
y1, y2, y3 は全て実数で、大小関係は、図形的考察により、
y2が一番大きい。y1とy3は計算してみないと不明。
y1=z+z^8+z^7+z^18+z^11+z^12 = -1.2218761622631909348
y2=z^2+z^16+z^14+z^17+z^3+z^5 = 2.5070186440929762999
y3=z^4+z^13+z^9+z^15+z^6+z^10 = -2.2851424818297853656
∴ y3<y1<0<y2
y=g-1/3 とおくと、
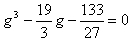 p=-19/3, q=-133/27
(q/2)^2+(p/3)^3=-361/108=-3.19^2/18^2
u^3,v^3= 133/54 +/- sqrt(-3.19^2/18^2)
p=-19/3, q=-133/27
(q/2)^2+(p/3)^3=-361/108=-3.19^2/18^2
u^3,v^3= 133/54 +/- sqrt(-3.19^2/18^2)
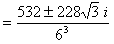 u+v = 2.8403519774263096322=g2
uw^2+vw=-0.8885428289298576011=g1
uw+vw^2=-1.9518091484964520309=g3
y1=g1-1/3
u+v = 2.8403519774263096322=g2
uw^2+vw=-0.8885428289298576011=g1
uw+vw^2=-1.9518091484964520309=g3
y1=g1-1/3
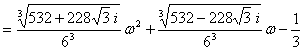 y2=g2-1/3
y2=g2-1/3
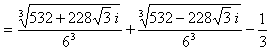 次に y1 を3分割(2つおき)
f1={1,18}
f2={8,11}
f3={7,12}
f1+f2+f3=y1, f2f3+f3f1+f1f2=(計算すると)=-y2-1, f1f2f3=(計算すると)=y2+2
よって、f1, f2, f3 は、
f^3-y1f^2-(y2+1)f-(y2+2)=0
の解
f1, f2, f3の大小関係は、図形的考察により、
f3<f2<0<f1
g=f-y1/3 とおくと、f=g+y1/3
f^3-y1f^2-(y2+1)f-(y2+2)
=g^3-(y1^2/3+y2+1)g-(2y1^3/27+y1y2/3+y1/3+y2+2)=0
p=-(y1^2/3+y2+1)
q=-(2y1^3/27+y1y2/3+y1/3+y2+2)
U=-(q/2)+sqrt((q/2)^2+(p/3)^3)
V=-(q/2)-sqrt((q/2)^2+(p/3)^3)
g1=cbrt(U)+cbrt(V)
g2=cbrt(U)w^2+cbrt(V)w
g3=cbrt(U)w+cbrt(V)w^2
f1=g1+y1/3
f1=z+z18=z+1/z=2Re(z)=2cos(2pi/19)
より、cos(2pi/19) を求めることができる。
----[n=19 の場合の概略:ここまで]----
----[n=37 の場合の概略:ここから]----
z から始めて、2乗していく
z, z^2, z^4, z^8, z^16, z^32, z^27, z^17, z^34, z^31, z^25, z^13,
z^26, z^15, z^30, z^23, z^9, z^18, z^36, z^35, z^33, z^29, z^21, z^5,
z^10, z^20, z^3, z^6, z^12, z^24, z^11, z^22, z^7, z^14, z^28, z^19,
2個おきに足す
y1=z+z^8+z^27+z^31+z^26+z^23+z^36+z^29+z^10+z^6+z^11+z^14
y2=z^2+z^16+z^17+z^25+z^15+z^9+z^35+z^21+z^20+z^12+z^22+z^28
y3=z^4+z^32+z^34+z^13+z^30+z^18+z^33+z^5+z^3+z^24+z^7+z^19
y1+y2+y3=-1
y1y2+y2y3+y3y1=(計算すると)
=12(z+z^2+...+z^36)
= -12
y1y2y3=(計算すると)
= 36+47(1,2,...,36)
= -11
よって、y1, y2, y3 は、
次に y1 を3分割(2つおき)
f1={1,18}
f2={8,11}
f3={7,12}
f1+f2+f3=y1, f2f3+f3f1+f1f2=(計算すると)=-y2-1, f1f2f3=(計算すると)=y2+2
よって、f1, f2, f3 は、
f^3-y1f^2-(y2+1)f-(y2+2)=0
の解
f1, f2, f3の大小関係は、図形的考察により、
f3<f2<0<f1
g=f-y1/3 とおくと、f=g+y1/3
f^3-y1f^2-(y2+1)f-(y2+2)
=g^3-(y1^2/3+y2+1)g-(2y1^3/27+y1y2/3+y1/3+y2+2)=0
p=-(y1^2/3+y2+1)
q=-(2y1^3/27+y1y2/3+y1/3+y2+2)
U=-(q/2)+sqrt((q/2)^2+(p/3)^3)
V=-(q/2)-sqrt((q/2)^2+(p/3)^3)
g1=cbrt(U)+cbrt(V)
g2=cbrt(U)w^2+cbrt(V)w
g3=cbrt(U)w+cbrt(V)w^2
f1=g1+y1/3
f1=z+z18=z+1/z=2Re(z)=2cos(2pi/19)
より、cos(2pi/19) を求めることができる。
----[n=19 の場合の概略:ここまで]----
----[n=37 の場合の概略:ここから]----
z から始めて、2乗していく
z, z^2, z^4, z^8, z^16, z^32, z^27, z^17, z^34, z^31, z^25, z^13,
z^26, z^15, z^30, z^23, z^9, z^18, z^36, z^35, z^33, z^29, z^21, z^5,
z^10, z^20, z^3, z^6, z^12, z^24, z^11, z^22, z^7, z^14, z^28, z^19,
2個おきに足す
y1=z+z^8+z^27+z^31+z^26+z^23+z^36+z^29+z^10+z^6+z^11+z^14
y2=z^2+z^16+z^17+z^25+z^15+z^9+z^35+z^21+z^20+z^12+z^22+z^28
y3=z^4+z^32+z^34+z^13+z^30+z^18+z^33+z^5+z^3+z^24+z^7+z^19
y1+y2+y3=-1
y1y2+y2y3+y3y1=(計算すると)
=12(z+z^2+...+z^36)
= -12
y1y2y3=(計算すると)
= 36+47(1,2,...,36)
= -11
よって、y1, y2, y3 は、
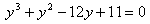 の解。
図形的考察により、y1, y2, y3 は実数。
y2<0<y1<y3
y1= 1.1576115578454257508 : uw^2+vw
y2=-4.3447123654518349673 : uw+vw^2
y3= 2.1871008076064091905 : u+v
の解。
図形的考察により、y1, y2, y3 は実数。
y2<0<y1<y3
y1= 1.1576115578454257508 : uw^2+vw
y2=-4.3447123654518349673 : uw+vw^2
y3= 2.1871008076064091905 : u+v
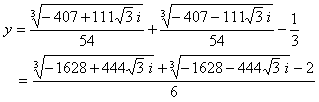 y1を3つに分ける
t1=z+z^31+z^36+z^6
t2=z^8+z^26+z^29+z^11
t3=z^27+z^23+z^10+z^14
t1+t2+t3=y1
t1t2+t2t3+t3t1=(計算すると)
= -1+y2
t1t2t3=(計算すると)
= 2-y1
よって、t1, t2, t3 は、
t^3-y1t^2+(-1+y2)t-(2-y1)=0
の根。t1, t2, t3は全て実数であり、大小関係は図形的考察により、
t3<t2<t1
t1=3.0198463878098802958
t2=-0.1642870025616481232
t3=-1.6979478274028064217
y3を3つに分ける
s1=z^4+z^13+z^33+z^24 : (= 0.366805156028305778)
s2=z^32+z^30+z^5+z^7 : (= 2.0670624023407800998)
s3=z^34+z^18+z^3+z^19 : (=-0.2467667507626766873)
s1+s2+s3=y3
s1s2+s2s3+s3s1=(計算すると)
=(y2+y3)+2y1
= -1+y1
s1s2s3=(計算すると)
=3+2(y1+y2)
t1を2つに分ける
w1=z+z^36
w2=z^6+z^31
w1+w2=t1
w1w2=(計算すると)=s2
よって、w1, w2 は、
w^2-t1w+s2=0 の解
z は、
w1=z+z^36=z+1/z から解ける
----[n=37 の場合の概略:ここまで]----
(n=73, 97 の場合は省略)
これらの解に半角公式、1/3角公式を適用することにより、
n=13, 26, 52,
n=39, 78
n=19, 38, 76
n=57
n=37, 74
n=73
n=97
の場合が得られる。
y1を3つに分ける
t1=z+z^31+z^36+z^6
t2=z^8+z^26+z^29+z^11
t3=z^27+z^23+z^10+z^14
t1+t2+t3=y1
t1t2+t2t3+t3t1=(計算すると)
= -1+y2
t1t2t3=(計算すると)
= 2-y1
よって、t1, t2, t3 は、
t^3-y1t^2+(-1+y2)t-(2-y1)=0
の根。t1, t2, t3は全て実数であり、大小関係は図形的考察により、
t3<t2<t1
t1=3.0198463878098802958
t2=-0.1642870025616481232
t3=-1.6979478274028064217
y3を3つに分ける
s1=z^4+z^13+z^33+z^24 : (= 0.366805156028305778)
s2=z^32+z^30+z^5+z^7 : (= 2.0670624023407800998)
s3=z^34+z^18+z^3+z^19 : (=-0.2467667507626766873)
s1+s2+s3=y3
s1s2+s2s3+s3s1=(計算すると)
=(y2+y3)+2y1
= -1+y1
s1s2s3=(計算すると)
=3+2(y1+y2)
t1を2つに分ける
w1=z+z^36
w2=z^6+z^31
w1+w2=t1
w1w2=(計算すると)=s2
よって、w1, w2 は、
w^2-t1w+s2=0 の解
z は、
w1=z+z^36=z+1/z から解ける
----[n=37 の場合の概略:ここまで]----
(n=73, 97 の場合は省略)
これらの解に半角公式、1/3角公式を適用することにより、
n=13, 26, 52,
n=39, 78
n=19, 38, 76
n=57
n=37, 74
n=73
n=97
の場合が得られる。
任意の n に対し、n-1 までの解がわかっている場合、 n についての解を求めることができることが知られている。 残っているもののうち最小の n=11 の場合について、Vandermondo の方法により求める。 この場合、5次方程式を解くことになる。 結果だけ示すと、ただし、複号、A, B は、 Δ' + + - A=20, B=25 Δ'' - + + A=25, B=20 Δ''' - - + A=25, B=20 Δ'''' + - - A=20, B=25 5乗根は Δ' = p.v. * exp(2π.i*3/5) = -2.6361055643248352116 -2.0126965627574470745.i Δ'' = p.v. * exp(2π.i*3/5) = -2.0701620998310706343 -2.5912215035428778155.i Δ''' = p.v. * exp(2π.i*2/5) = -2.070162099831070634 +2.5912215035428778156.i Δ''''= p.v. * exp(2π.i*2/5) = -2.6361055643248352115 +2.0126965627574470746.i の値を選択する。sin(2pi/11) は、sqrt(1-cos(2pi/11)^2) ----[n=11 の場合の概略:ここから]---- z^11-1=0 z^10+z^9+z^8+...+z+1=0 t=z+1/z とおく。t^2, t^3, t^4, t^5 を計算すると、 t^2=z^2+1/z^2+2 t^3=z^3+1/z^3+3(z+1/z)=z^3+1/z^3+3t t^4=z^4+1/z^4+4(z^2+1/z^2)+6=z^4+1/z^4+4t^2-2 t^5=z^5+1/z^5+5(z^3+1/z^3)+10(z+1/z)=z^5+1/z^5+5t^3-5t これを代入する (z^5+1/z^5)+(z^4+1/z^4)+(z^3+1/z^3)+(z^2+1/z^2)+(z+1/z)+1 =t^5-5t^3+5t+t^4-4t^2+2+t^3-3t+t^2-2+t+1 =t^5+t^4-4t^3-3t^2+3t+1=0 この5つの解は、 t=z+1/z=2cos(2π.k/11), k=1,2,3,4,5 a=2cos(2pi/11)=z+z10=z+1/z b=2cos(4pi/11)=z2+z9=z^2+1/z^2 c=2cos(6pi/11)=z3+z8=z^3+1/z^3 d=2cos(8pi/11)=z4+z7=z^4+1/z^4 e=2cos(10pi/11)=z5+z6=z^5+1/z^5 z から始まり2乗していく。 z, z^2, z^4, z^8, z^16=5, z^10, z^20=z^9, z^18=z^7, z^14=z^3, z^6, z^12=z a => b => d => c => e => a という置換は、解 {a,b,c,d,e} を保存する(自己同型写像となっている)。 a^2, ... ,e^2 を計算。 a^2=(z+1/z)^2=z^2+1/z^2+2=b+2 b^2=d+2 c^2=e+2 d^2=c+2 e^2=a+2 次に、a, ... ,e 任意の2個の積を計算。これはやはり a, ... ,e の一次式となる。 (今は省略するが、後の計算で、次数を下げるための簡略式として必要になってくる) w を1の原始5乗根とする。w=exp(2π.i/5) w^2=exp(4pi.i/5), w^3=exp(6pi.i/5), w^4=exp(8pi.i/5), w^5=1 V1, ... , V4 を次のように定義 V1 = a + bw + dw^2 + cw^3 + ew^4 V2 = a + bw^2 + dw^4 + cw + ew^3 V3 = a + bw^3 + dw + cw^4 + ew^2 V4 = a + bw^4 + dw^3 + cw^2 + ew (a,...,e の順序に注意) もう1個、 a + b + c + d + e = -1 という関係式がある(a,...,e の定義より明らか)。 これは a, ... ,e の連立方程式であり、 a = (1+ V1+ V2+ V3+ V4)/5 b = (1+w^4V1+w^3V2+w^2V3+ wV4)/5 c = (1+w^3V1+ wV2+w^4V3+w^2V4)/5 d = (1+w^2V1+w^4V2+ wV3+w^3V4)/5 e = (1+ wV1+w^2V2+w^3V3+w^4V4)/5 V1, ... , V4 は、実は w(既知の値)の式で表すことができる。 a, ... ,e を a => b => d => c => e => a と置き換えていく置換をσとし、V1について適用すると、 V1 = a + bw + dw^2 + cw^3 + ew^4 σ(V1)= b + dw + cw^2 + ew^3 + aw^4 = aw^4 + b + dw + cw^2 + ew^3 = aw^4 + bw^5 + dw^6 + cw^7 + ew^8 (w^5=1 なので) = w^4(a + bw + dw^2 + cw^3 + ew^4) = w^4V1 よって、σ(V1^5)=σ(V1)^5=V1^5。つまり、σはV1^5に対して不変。 V2, V3, V4 についても、5乗は不変。5乗が不変ということは、 V1^5, V2^5, V3^5, V4^5 の式から a,b,c,d,e が消えることを意味する。 V1^5=(a+bw+dw^2+cw^3+ew^4)^5 = ...(V1を掛けるごとに、上記の簡略式で、a,...,e の次数を下げていく) = w だけの式となる(a,b,c,d,e は消える) V2^5,...,V4^5 は、w => w^2 => w^4 => w^3 => w の置き換えで、 V1 => V2 => V4 => V3 => V1 の順に得られる。 V1^5,...,V4^5 の式に w の値を代入すると、V1^5,...,V4^5 のベキ根表現が得られる。 これらの5乗根をとることにより、V1,...,V4 の値が得られる。 (ただし、5個の5乗根のうち、どの値を取るべきかを考える必要あり) これら V1,...,V4 を a = (1+ V1+ V2+ V3+ V4)/5 b = (1+w^4V1+w^3V2+w^2V3+ wV4)/5 c = (1+w^3V1+ wV2+w^4V3+w^2V4)/5 d = (1+w^2V1+w^4V2+ wV3+w^3V4)/5 e = (1+ wV1+w^2V2+w^3V3+w^4V4)/5 に代入し、a,...,e が得られる。 a=2cos(2pi/11)=z+z10=z+1/z より、cos(2pi/11) が得られる。 ----[n=11 の場合の概略:ここまで]---- n=11に半角公式、1/3角公式を適用することにより、 n=22, 44, 88 n=33, 66 n=99 の場合を求めることができる。 一般の5次方程式の解法については、 "Quintic Equation", Wolfram Math World, http://mathworld.wolfram.com/QuinticEquation.html
100以下で残っている n のうち、
n が偶数の時は、n/2 に対し半角公式を適用
n が3の倍数の時は、n/3 に対し1/3角公式を適用
で求めることができるので、残りは、
n=23, 25, 29, 31, 35, 41, 43, 47, 49, 53, 55, 59,
61, 65, 67, 71, 77, 79, 83, 85, 89, 91, 95
n=25 : 5 * 5 : n= 5 に対し5乗根
n=35 : 5 * 7 : n= 7 に対し5乗根
n=49 : 7 * 7 : n= 7 に対し7乗根
n=55 : 5 * 11 : n=11 に対し5乗根
n=65 : 5 * 13 : n=13 に対し5乗根
n=77 : 7 * 11 : n=11 に対し7乗根
n=85 : 5 * 17 : n=17 に対し5乗根
n=91 : 7 * 13 : n=13 に対し7乗根
n=95 : 5 * 19 : n=19 に対し5乗根
Vandermondo の方法の場合、n-1 を素因数分解した最大因子が解くべき方程式となる。
n=23 : 22 = 2*11 : 11次方程式
n=29 : 28 = 2^2*7 : 7次方程式
n=31 : 30 = 2*3*5 : 5次方程式
n=41 : 40 = 2^3*5 : 5次方程式
n=43 : 42 = 2*3*7 : 7次方程式
n=47 : 46 = 2*23 : 23次方程式
n=53 : 52 = 2^2*13 : 13次方程式
n=59 : 58 = 2*29 : 29次方程式
n=61 : 60 = 2^2*3*5 : 5次方程式
n=67 : 66 = 2*3*11 : 11次方程式
n=71 : 70 = 2*5*7 : 7次方程式
n=79 : 78 = 2*3*13 : 13次方程式
n=83 : 82 = 2*41 : 41次方程式
n=89 : 88 = 2^3*11 : 11次方程式
残っている n のうち、最小の値は 23。この場合、11次方程式を解く必要がある。
5次の次、7次方程式を解く必要が出てくる最小の値は、n=29。
この場合、4個ずつのペアリング 7個についての方程式となるはず。
一番大変なのは、n=84 の場合で、41次方程式を解く必要がある。
z^n-1=0 は正多角形の作図問題と関係がある。
定木とコンパスにより、2のベキ乗拡大の範囲の無理数を作図することができる。
これにより、
n=4, 8, 16, 32, 64
n=3, 6, 12, 24, 48, 96
n=5, 10, 20, 40, 80
n=17, 34, 68
大きさ順に並べると、
n=3, 4, 5, 6, 8, 10, 12, 16, 17, 20, 24, 32, 34, 40, 48, 64, 68, 80, 96
の多角形は、定木とコンパスで作図できる。
折り紙の場合は、放物線と円の交点を求めることができるので、
任意の3次方程式の解を求めることができる(3のベキ乗拡大)。
これにより、任意の角の3等分が可能となる。
よって、上記に加えて、
n=9, 18, 36, 72
n=27, 54
n=81
n=15, 30, 60
n=45, 90
n=51
3次方程式を解くことにより、
n=7, 14, 28, 56
n=21, 42, 84
n=63
n=13, 26, 52,
n=39, 78
n=19, 38, 76
n=57
n=37, 74
n=73
n=97
大きさ順に並べると、
n=3, 4, 5, 6, 7, 8, 9, 10, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 24, 26, 27, 28,
30, 32, 34, 36, 37, 38, 39, 40, 42, 45, 48, 51, 42, 54, 56, 57, 60, 63, 64, 68,
72, 73, 74, 76, 78, 80, 81, 84, 90, 96, 97
の多角形を、折り紙で作図できる。
よって、正20角形以下については(正11角形を除き)全て、折り紙で折ることができる。
ζp : 1 の p 乗根
g : p の原始根
とする。
[定義] Gaussian period : ζのベキ乗の和
f, k に対し、f|p-1, k≠0 の時、period (f,k) を以下のように定義
f-1
(f,k) = Σ (ζ^(kg^em))
m=0
ここで、e=(p-1)/f, ベキ (em, g^em, kg^em) は mod p の値とする。
f を period (f,k) の長さ(length)と呼ぶ(項の個数となる)
length 1, (1,k) は、ζ^k
例.f=p-1, k=1 の時、e=(p-1)/(p-1)=1
p-2
(p-1,1) = Σ (ζ^(g^m))
m=0
= ζ^(g^0) + ζ^(g^1) + ζ^(g^2) + ... + ζ^(g^p-2)
g は p の原始根なので、g^m (m=0, 1, ... , p-2) は、
1 から p-1 までの (p-1)個全部を1回ずつ取る。
よって、
= ζ + ζ^2 + ζ^3 + ... + ζ^(p-1)
= -1
上記の n=17 の場合、原始根 g=3 に対する Gaussian period を使っている。
f=8 (=(17-1)/2)
(8,k)=z^(k3^0)+z^(k3^2)+z^(k3^4)+z^(k3^6)+z^(k3^8)+z^(k3^10)+z^(k3^12)+z^(k3^14)
=z^k.1+z^k.9+z^k.13+z^k.15+z^k.16+z^k.8+z^k.4+z^k.2
(8,1)=z^1+z^9+z^13+z^15+z^16+z^8+z^4+z^2
(8,3)=z^3.1+z^3.9+z^3.13+z^3.15+z^3.16+z^3.8+z^3.4+z^3.2
=z^3+z^10+z^5+z^11+z^14+z^7+z^12+z^6
f=4 (=8/2, =(17-1)/4)
(4,k)=z^(k3^0)+z^(k3^4)+z^(k3^8)+z^(k3^12)
=z^k.1+z^k.13+z^k.16+z^k.4
(4,1)=z^1+z^13+z^16+z^4
(4,3)=z^3.1+z^3.13+z^3.16+z^3.4
=z^3+z^5+z^14+z^12
(4,3^2)=z^(3^2.3^0)+z^(3^2.3^4)+z^(3^2.3^8)+z^(3^2.3^12)
=z^9+z^15+z^8+z^2
(4,3^3)=z^(3^3.3^0)+z^(3^3.3^4)+z^(3^3.3^8)+z^(3^3.3^12)
=z^10+z^11+z^7+z^6
f=2 (=4/2, =(17-1)/8)
(2,k)=z^(k3^0)+z^(k3^8)
=z^k.1+z^k.16
(2,3^0)=z^1+z^16
(2,3^1)=z^(3^1.3^0)+z^(3^1.3^8)=z^3+z^14
(2,3^2)=z^(3^2.3^0)+z^(3^2.3^8)=z^9+z^8
(2,3^3)=z^(3^3.3^0)+z^(3^3.3^8)=z^10+z^7
(2,3^4)=z^(3^4.3^0)+z^(3^4.3^8)=z^13+z^4
(2,3^5)=z^(3^5.3^0)+z^(3^5.3^8)=z^5+z^12
(2,3^6)=z^(3^6.3^0)+z^(3^6.3^8)=z^15+z^2
(2,3^7)=z^(3^7.3^0)+z^(3^7.3^8)=z^11+z^6
上記の n=13 の場合、原始根 g=2 に対する Gaussian period を使っている。
f=6 (=(13-1)/2)
(6,k)=z^(k2^0)+z^(k2^2)+z^(k2^4)+z^(k2^6)+z^(k2^8)+z^(k2^10)
=z^k.1+z^k.4+z^k.3+z^k.12+z^k.9+z^k.10
(6,1)=z^1+z^4+z^3+z^12+z^9+z^10
(6,2)=z^(2.2^0)+z^(2.2^2)+z^(2.2^4)+z^(2.2^6)+z^(2.2^8)+z^(2.2^10)
=z^2+z^8+z^6+z^11+z^5+z^7
f=2 (=6/3, (13-1)/6)
(2,k)=z^(k2^0)+z^(k2^6)
=z^k.1+z^k.12
(2,2^0)=z^1+z^12
(2,2^1)=z^(2.2^0)+z^(2.2^6)=z^2+z^11
(2,2^2)=z^(2^2.2^0)+z^(2^2.2^6)=z^4+z^9
(2,2^3)=z^(2^3.2^0)+z^(2^3.2^6)=z^8+z^5
(2,2^4)=z^(2^4.2^0)+z^(2^4.2^6)=z^3+z^10
(2,2^5)=z^(2^5.2^0)+z^(2^5.2^6)=z^6+z^7
上記の n=19 の場合、原始根 g=2 に対する Gaussian period を使っている。
f=6 (=(19-1)/3)
(6,k)=z^(k2^0)+z^(k2^3)+z^(k2^6)+z^(k2^9)+z^(k2^12)+z^(k2^15)
=z^k.1+z^k.8+z^k.7+z^k.18+z^k.11+z^k.12
(6,2^0)=z^1+z^8+z^7+z^18+z^11+z^12
(6,2^1)=z^(2^1.2^0)+z^(2^1.2^3)+z^(2^1.2^6)+z^(2^1.2^9)+z^(2^1.2^12)+z^(2^1.2^15)
=z^2+z^16+z^14+z^17+z^3+z^5
(6,2^2)=z^(2^2.2^0)+z^(2^2.2^3)+z^(2^2.2^6)+z^(2^2.2^9)+z^(2^2.2^12)+z^(2^2.2^15)
=z^4+z^13+z^9+z^15+z^6+z^10
f=2 (=6/2, =(19-1)/9)
(2,k)=z^(k2^0)+z^(k2^9)
=z^k.1+z^k.18
(2,2^0)=z^1+z^18
(2,2^1)=z^(2^1.2^0)+z^(2^1.2^9)=z^2+z^17
(2,2^2)=z^(2^2.2^0)+z^(2^2.2^9)=z^4+z^15
(2,2^3)=z^(2^3.2^0)+z^(2^3.2^9)=z^8+z^11
(2,2^4)=z^(2^4.2^0)+z^(2^4.2^9)=z^16+z^3
(2,2^5)=z^(2^5.2^0)+z^(2^5.2^9)=z^13+z^6
(2,2^6)=z^(2^6.2^0)+z^(2^6.2^9)=z^7+z^12
(2,2^7)=z^(2^7.2^0)+z^(2^7.2^9)=z^14+z^5
(2,2^8)=z^(2^8.2^0)+z^(2^8.2^9)=z^9+z^10
上記の n=37 の場合、原始根 g=2 に対する Gaussian period を使っている。
f=12 (=(37-1)/3)
(12,k)=z^(k2^0)+z^(k2^3)+z^(k2^6)+z^(k2^9)+z^(k2^12)+z^(k2^15)+z^(k2^18)+z^(k2^21)+z^(k2^24)+z^(k2^27)+z^(k2^30)+z^(k2^33)
=z^k.1+z^k.8+z^k.27+z^k.31+z^k.26+z^k.23+z^k.36+z^k.29+z^k.10+z^k.6+z^k.11+z^k.14
(12,1)=z^1+z^8+z^27+z^31+z^26+z^23+z^36+z^29+z^10+z^6+z^11+z^14
(12,2)=z^2.1+z^2.8+z^2.27+z^2.31+z^2.26+z^2.23+z^2.36+z^2.29+z^2.10+z^2.6+z^2.11+z^2.14
=z^2+z^16+z^17+z^25+z^15+z^9+z^35+z^21+z^20+z^12+z^22+z^28
(12,4)=z^4.1+z^4.8+z^4.27+z^4.31+z^4.26+z^4.23+z^4.36+z^4.29+z^4.10+z^4.6+z^4.11+z^4.14
=z^4+z^32+z^34+z^13+z^30+z^18+z^33+z^5+z^3+z^24+z^7+z^19
f=4 (=12/3, =(37-1)/9)
(4,k)=z^(k2^0)+z^(k2^9)+z^(k2^18)+z^(k2^27)
=z^k.1+z^k.31+z^k.36+z^k.6
(4,2^0)=z^1+z^31+z^36+z^6
(4,2^1)=z^2+z^25+z^35+z^12
(4,2^2)=z^4+z^13+z^33+z^24
(4,2^3)=z^8+z^26+z^29+z^11
(4,2^4)=z^16+z^15+z^21+z^22
(4,2^5)=z^32+z^30+z^5+z^7
(4,2^6)=z^27+z^23+z^10+z^14
(4,2^7)=z^17+z^9+z^20+z^28
(4,2^8)=z^34+z^18+z^3+z^19
f=2 は省略。
この要領で、p=73, 97 の式を書き出しておく(ベキだけを表記)。
p=73, g=5
72-(3)-24-(3)-8-(2)-4-(2)-2-(2)-1
f=24
p0=(24,5^0)={1, 52, 3, 10, 9, 30, 27, 17, 8, 51, 24, 7, 72, 21, 70, 63, 64, 43, 46, 56, 65, 22, 49, 66}
p1=(24,5^1)={5, 41, 15, 50, 45, 4, 62, 12, 40, 36, 47, 35, 68, 32, 58, 23, 28, 69, 11, 61, 33, 37, 26, 38}
p2=(24,5^2)={25, 59, 2, 31, 6, 20, 18, 60, 54, 34, 16, 29, 48, 14, 71, 42, 67, 53, 55, 13, 19, 39, 57, 44}
p0+p1+p2= -1
p1p2+p2p0+p0p1= -24
p0p1p2=216-189=27
p^3+p^2-24p-27=0
f=8
q0=(8,5^0)={1, 10, 27, 51, 72, 63, 46, 22}
q1=(8,5^1)={5, 50, 62, 36, 68, 23, 11, 37}
q2=(8,5^2)={25, 31, 18, 34, 48, 42, 55, 39}
q3=(8,5^3)={52, 9, 17, 24, 21, 64, 56, 49}
q4=(8,5^4)={41, 45, 12, 47, 32, 28, 61, 26}
q5=(8,5^5)={59, 6, 60, 16, 14, 67, 13, 57}
q6=(8,5^6)={3, 30, 8, 7, 70, 43, 65, 66}
q7=(8,5^7)={15, 4, 40, 35, 58, 69, 33, 38}
q8=(8,5^8)={2, 20, 54, 29, 71, 53, 19, 44}
q0+q3+q6=p0
q3q6+q6q0+q0q3=3p0+p1+4p2
q0q3q6=1
q^3-p0q^2+(3p0+p1+4p2)q-1=0
f=4
r0=(4,5^0)={1, 27, 72, 46}
r1=(4,5^1)={5, 62, 68, 11}
r2=(4,5^2)={25, 18, 48, 55}
r3=(4,5^3)={52, 17, 21, 56}
r4=(4,5^4)={41, 12, 32, 61}
r5=(4,5^5)={59, 60, 14, 13}
r6=(4,5^6)={3, 8, 70, 65}
r7=(4,5^7)={15, 40, 58, 33}
r8=(4,5^8)={2, 54, 71, 19}
r9=(4,5^9)={10, 51, 63, 22}
r10=(4,5^10)={50, 36, 23, 37}
r11=(4,5^11)={31, 34, 42, 39}
r12=(4,5^12)={9, 24, 64, 49}
r13=(4,5^13)={45, 47, 28, 26}
r14=(4,5^14)={6, 16, 67, 57}
r15=(4,5^15)={30, 7, 43, 66}
r16=(4,5^16)={4, 35, 69, 38}
r17=(4,5^17)={20, 29, 53, 44}
r0+r9=q0
r0r9=q1+q3
r^2-q0r+(q1+q3)=0
p=97, g=5
96-(3)-32-(2)-16-(2)-8-(2)-4-(2)-2-(2)-1
f=32
p0=(32,5^0)={1, 28, 8, 30, 64, 46, 27, 77, 22, 34, 79, 78, 50, 42, 12, 45, 96, 69, 89, 67, 33, 51, 70, 20, 75, 63, 18, 19, 47, 55, 85, 52}
p1=(32,5^1)={5, 43, 40, 53, 29, 36, 38, 94, 13, 73, 7, 2, 56, 16, 60, 31, 92, 54, 57, 44, 68, 61, 59, 3, 84, 24, 90, 95, 41, 81, 37, 66}
p2=(32,5^2)={25, 21, 6, 71, 48, 83, 93, 82, 65, 74, 35, 10, 86, 80, 9, 58, 72, 76, 91, 26, 49, 14, 4, 15, 32, 23, 62, 87, 11, 17, 88, 39}
p0+p1+p2= -1
p1p2+p2p0+p0p1= -32
p0p1p2= -337
p^3+p^2-32p+337=0
f=16
q0=(16,5^0)={1, 8, 64, 27, 22, 79, 50, 12, 96, 89, 33, 70, 75, 18, 47, 85}
q1=(16,5^1)={5, 40, 29, 38, 13, 7, 56, 60, 92, 57, 68, 59, 84, 90, 41, 37}
q2=(16,5^2)={25, 6, 48, 93, 65, 35, 86, 9, 72, 91, 49, 4, 32, 62, 11, 88}
q3=(16,5^3)={28, 30, 46, 77, 34, 78, 42, 45, 69, 67, 51, 20, 63, 19, 55, 52}
q4=(16,5^4)={43, 53, 36, 94, 73, 2, 16, 31, 54, 44, 61, 3, 24, 95, 81, 66}
q5=(16,5^5)={21, 71, 83, 82, 74, 10, 80, 58, 76, 26, 14, 15, 23, 87, 17, 39}
q0+q3=p0
q0q3= 4p0+3p1+p2
q^2-p0q+(4p0+3p1+p2)=0
f=8
r0=(8,5^0)={1, 64, 22, 50, 96, 33, 75, 47}
r1=(8,5^1)={5, 29, 13, 56, 92, 68, 84, 41}
r2=(8,5^2)={25, 48, 65, 86, 72, 49, 32, 11}
r3=(8,5^3)={28, 46, 34, 42, 69, 51, 63, 55}
r4=(8,5^4)={43, 36, 73, 16, 54, 61, 24, 81}
r5=(8,5^5)={21, 83, 74, 80, 76, 14, 23, 17}
r6=(8,5^6)={8, 27, 79, 12, 89, 70, 18, 85}
r7=(8,5^7)={40, 38, 7, 60, 57, 59, 90, 37}
r8=(8,5^8)={6, 93, 35, 9, 91, 4, 62, 88}
r9=(8,5^9)={30, 77, 78, 45, 67, 20, 19, 52}
r10=(8,5^10)={53, 94, 2, 31, 44, 3, 95, 66}
r11=(8,5^11)={71, 82, 10, 58, 26, 15, 87, 39}
r0+r6=q0
r0r6=q1+q2+q4+q5
r^2-q0r+(q1+q2+q4+q5)=0
f=4
s0=(4,5^0)={1, 22, 96, 75}
s1=(4,5^1)={5, 13, 92, 84}
s2=(4,5^2)={25, 65, 72, 32}
s3=(4,5^3)={28, 34, 69, 63}
s4=(4,5^4)={43, 73, 54, 24}
s5=(4,5^5)={21, 74, 76, 23}
s6=(4,5^6)={8, 79, 89, 18}
s7=(4,5^7)={40, 7, 57, 90}
s8=(4,5^8)={6, 35, 91, 62}
s9=(4,5^9)={30, 78, 67, 19}
s10=(4,5^10)={53, 2, 44, 95}
s11=(4,5^11)={71, 10, 26, 87}
s12=(4,5^12)={64, 50, 33, 47}
s13=(4,5^13)={29, 56, 68, 41}
s14=(4,5^14)={48, 86, 49, 11}
s15=(4,5^15)={46, 42, 51, 55}
s16=(4,5^16)={36, 16, 61, 81}
s17=(4,5^17)={83, 80, 14, 17}
s18=(4,5^18)={27, 12, 70, 85}
s19=(4,5^19)={38, 60, 59, 37}
s20=(4,5^20)={93, 9, 4, 88}
s21=(4,5^21)={77, 45, 20, 52}
s22=(4,5^22)={94, 31, 3, 66}
s23=(4,5^23)={82, 58, 15, 39}
s0+s12=r0
s0s12=r2+r3
t0={1,96}, t12={22,75}
t0+t12=s0
t0t12=s5
t^2-s0t+s5=0
[1] Jean-Pierre Tignol, 新妻 弘 訳, "代数方程式のガロア理論(原題:Galois' Theory of Algebraic Equations)", 共立出版, 2005/03/15
[2] C. F. Gauss, 高瀬 正仁 訳, "ガウス整数論(原題:Disquisitiones Arithmeticae)", 朝倉書店, 1995
| index (Japanese) |
|---|